Os limites de velocidade para fenômenos quânticos foram estendidos para objetos de tamanho macro
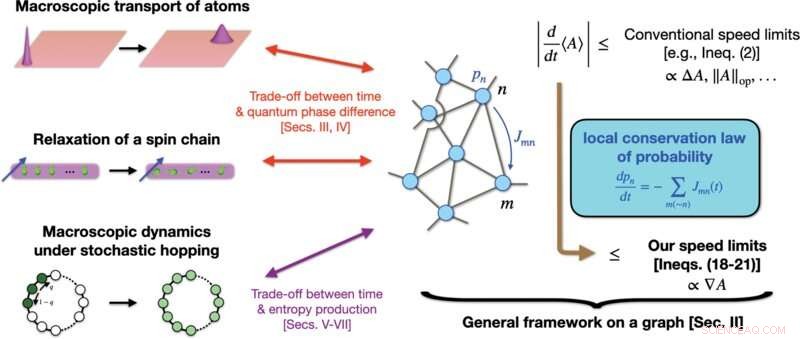
Ilustração esquemática de nossas realizações. Estabelecemos uma estrutura geral para derivar limites de velocidade qualitativamente mais rígidos de uma quantidade A do que muitos convencionais, que dependem de toda a gama de A , como ΔA ou ∥A ∥op . Nossa estratégia é mapear dinâmicas gerais de nosso interesse para dinâmicas em um gráfico, onde usamos a conservação local da probabilidade. Em contraste com os limites convencionais, nossos limites de velocidade envolvem o gradiente ∇A de A no gráfico, o que pode reduzir significativamente o limite quando ∇A ≪ΔA ou ∥A ∥op . Quando aplicada a sistemas quânticos macroscópicos (como transporte macroscópico de átomos ou relaxamento de uma cadeia de spin localmente perturbada), nossa teoria indica uma nova relação de troca entre o tempo e a diferença de fase quântica. Quando aplicada à dinâmica estocástica macroscópica, incluindo a quântica, nossa teoria indica uma relação de troca entre tempo e quantidades como a produção de entropia. Crédito:PRX Quantum (2022). DOI:10.1103/PRXQuantum.3.020319
Uma expressão para a velocidade máxima na qual as mudanças nos sistemas macroscópicos podem ocorrer foi derivada por um físico teórico do RIKEN. Isso aprofundará nossa compreensão dos fenômenos quânticos em sistemas que não estão em equilíbrio.
Um dos aspectos mais difíceis da mecânica quântica de entender é o princípio da incerteza de Heisenberg, que afirma que não é possível determinar simultaneamente a posição e o momento de um objeto. Em outras palavras, quanto mais precisamente a posição de uma partícula é determinada, mais amplo se torna o alcance de seu momento possível (e vice-versa).
Em 1945, dois físicos, Leonid Mandelstam e Igor Tamm, focaram em outro tipo de relação de incerteza, a saber, entre tempo e flutuação de energia, e mostraram que as transições em sistemas quânticos não acontecem instantaneamente; em vez disso, a velocidade na qual uma transição ocorre é limitada por uma quantidade determinada por quanto a energia do sistema flutua.
Muitos outros chamados limites de velocidade quântica foram derivados posteriormente, que ajudaram a entender melhor a física dos sistemas quânticos e foram úteis em várias aplicações quânticas.
Mas grandes problemas surgem quando os limites de velocidade quântica são aplicados a sistemas macroscópicos. “Os limites de velocidade quântica anteriores, que são úteis para pequenos sistemas, normalmente se tornam sem sentido para transições macroscópicas”, observa Ryusuke Hamazaki, da Equipe de Pesquisa de Mecânica Estatística Quântica do Noequilibrium RIKEN Hakubi. "Por exemplo, os limites convencionais de velocidade quântica dão um limite superior infinito para a velocidade das transições em um gás composto de átomos."
Agora, Hamazaki conseguiu derivar um limite de velocidade quântica para transições em sistemas macroscópicos.
"Esta nova derivação fornece limites fundamentais que podem ser aplicados a vários tipos de fenômenos macroscópicos quânticos fora do equilíbrio", diz ele. "Espero que muitas leis e aplicações fundamentais relativas à dinâmica quântica macroscópica apareçam com base nos conceitos introduzidos neste estudo."
Hamazaki derivou o limite de velocidade quântica mais rigoroso desenvolvendo uma estrutura geral baseada na lei de conservação da probabilidade, um princípio fundamental da física.
Um resultado inesperado para Hamazaki foi a descoberta de uma nova relação de troca. "Em vez de uma relação de troca entre tempo e flutuação de energia, como no limite de Mandelstam-Tamm, encontrei uma entre o tempo e o gradiente da fase quântica - uma quantidade fundamental na física quântica."
Hamazaki agora pretende estender sua estratégia para ver se ela pode ser usada para derivar limites de velocidade quântica para quantidades como o crescimento do emaranhamento quântico.
+ Explorar mais Os limites de velocidade quântica não são realmente quânticos
