Quando os materiais curvos são achatados, a geometria simples pode prever os padrões de rugas que surgem
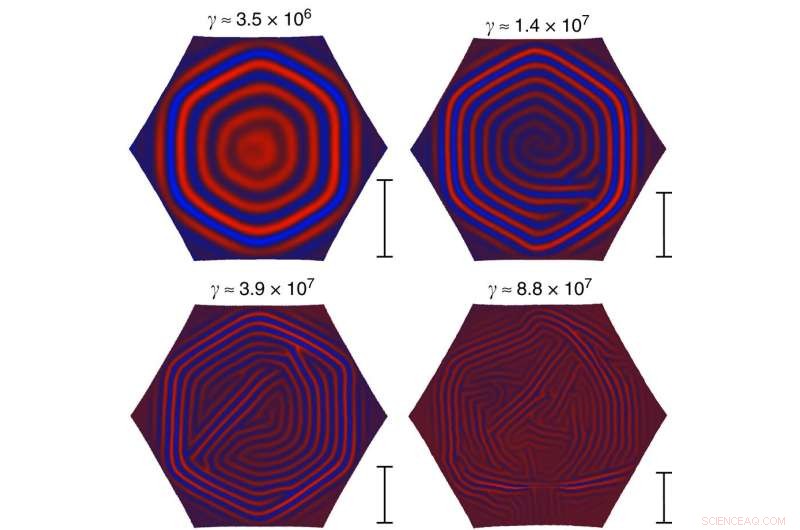
Dimensionamento do tamanho do domínio. Padrões típicos de rugas de equilíbrio em uma seção hexagonal de uma casca esférica fina em um substrato líquido. Todos os parâmetros de simulação são mantidos fixos, exceto a espessura da chapa. O número de Föppl–von Kármán γ do sistema é indicado acima de cada padrão. Enquanto o padrão superior esquerdo é claramente dividido em seis domínios, o aumento de γ parece diminuir o tamanho do domínio típico. A barra de escala à direita de cada padrão mostra a escala dos tamanhos de domínio típicos previstos pela equação (20), até um fator constante (apenas as razões entre as barras são significativas, pois a equação (20) sugere apenas a escala do tamanho típico e deixa o prefator desconhecido). Crédito:Comunicação da Natureza (2017). DOI:10.1038/ncoms15809
Um objeto que é intrinsecamente plano, digamos um pedaço de papel, pode ser moldado em um cilindro sem esticá-lo ou rasgá-lo. O mesmo não é verdade, no entanto, para algo intrinsecamente curvo como uma lente de contato. Quando comprimidos entre duas superfícies planas ou colocados na água, os objetos curvos se achatam, mas com rugas que se formam à medida que se dobram.
Agora, pesquisas da Universidade da Pensilvânia, da Universidade de Illinois Chicago (UIC) e da Universidade de Syracuse mostraram que, com alguma geometria simples, é possível prever os padrões dessas rugas, tanto onde elas se formarão quanto, em alguns casos, sua direção. As descobertas, publicadas em
Nature Physics , têm uma série de implicações, desde como os materiais interagem com a umidade e refletem a luz solar na natureza até a maneira como um eletrônico flexível pode se curvar.
"A beleza deste trabalho é o quão simples ele realmente é", diz Eleni Katifori, professora associada do Departamento de Física e Astronomia da Penn. "O que está por trás disso é muito complicado, a física que é traduzida por essas regras que encontramos, mas as regras em si são muito simples. É inspirador."
Encontro de mentes Desde seu Ph.D. trabalho, Katifori se interessou pela mecânica de como as membranas finas se curvam. Embora isso continuasse sendo uma curiosidade, seu caminho de pesquisa se voltou para redes de fluxo de fluido. Então, enquanto colaborava em um projeto com o colega da Penn Randall Kamien e o colega de pós-doutorado Hillel Aharoni, Katifori observou algo que ela não conseguia explicar na época. "Ou seja, notamos que as rugas se formam em domínios", diz ela.
Em outras palavras, quando uma superfície curva é achatada, acaba ficando com excesso de material e subsequentes rugas. Essas rugas surgem em padrões ou setores. "A questão tornou-se, por que as rugas se organizam dessa maneira?" diz Katifori. "Nós não entendemos o quão importante os domínios no enrugamento são realmente."
Em uma conferência em 2016, o matemático Ian Tobasco, professor assistente da UIC, ouviu Aharoni dar uma palestra sobre o assunto. "Foi a primeira vez que vi este sistema modelo sendo apresentado", diz Tobasco. "Eu pensei que isso fosse muito legal." Em meados de 2017, Katifori, Aharoni e colegas publicaram descobertas sobre o assunto na
Nature Communications , então em um workshop no final daquele ano, Tobasco conheceu Joseph Paulsen, de Siracusa, que apresentou dados preliminares sobre a experimentação que seu grupo havia feito com rugas.
No início de 2018, Tobasco começou a trabalhar seriamente em uma teoria matemática para rugas e, durante o almoço em uma conferência naquele verão, Katifori, Tobasco e Paulsen concordaram que compartilhavam um interesse nesse problema. Eles decidiram colaborar, com foco em analisar o quanto a forma física do material e a curvatura a partir da qual ele começa podem importar para os padrões de rugas.
Trabalhando com o problema Para alguns fundos, a curvatura pode ser positiva, como o arredondamento de uma bola de beisebol ou de um globo, ou negativa, como a sela de um cavalo ou o ponto em uma garrafa de vidro onde o gargalo encontra a base. Há também material plano, como um pedaço de papel.
Neste trabalho, os pesquisadores se concentraram em conchas curvadas positiva e negativamente.
De cada um, eles removeram formas básicas, como triângulos, quadrados e ovais. "Pense em um cortador de biscoitos. Digamos que eu pegue um objeto com uma curvatura positiva ou negativa, depois corte uma dessas formas e coloque-a no líquido", diz Katifori. Seria possível adivinhar os padrões de rugas e calcular a direção em que as rugas fluiriam? Para cada forma, Tobasco resolveria a teoria com base nos princípios fundamentais que ele havia elaborado e publicado, e então faria previsões.
Com base nessas descobertas, a pesquisadora de pós-doutorado Katifori e Penn, Desislava Todorova, realizou simulações, inserindo formas e parâmetros individuais em um programa de computador. Trabalho semelhante estava acontecendo no laboratório dirigido por Paulsen, professor assistente de física em Syracuse, por meio de experimentos que ele estava realizando em um filme de poliestireno 1.000 vezes mais fino que um pedaço de papel. "É feito do mesmo material que o amendoim embalado", diz Tobasco, "mas em vez da forma tridimensional de um amendoim embalado, imagine que é plano como uma folha".
Através das simulações, experimentação e muito para refinar o processo e expandir a teoria original, o trio começou a discernir que, aplicando princípios geométricos diretos, eles poderiam saber antecipadamente qual padrão as rugas teriam e por um subconjunto — o que eles descrevem como rugas "ordenadas" — em que direção eles correriam.
Os princípios geométricos Para explicar um desses princípios, Katifori usa um polígono de cinco lados. "Primeiro eu inscrevo um círculo no polígono", diz ela. "Os pontos onde esse círculo toca as bordas do polígono determinam onde eu desenho minhas linhas." Ela faz uma pausa para criar uma segunda forma dentro da primeira, esta com quatro lados desiguais; ela inicia cada linha onde o círculo e o polígono externo se encontram, conectando todas as quatro linhas internas. "Agora eu tenho um, dois, três, quatro, cinco domínios", ela continua, apontando o quinteto de seções recém-isoladas.
Para formas simples como esta, as seções externas conterão rugas ordenadas, que são organizadas e ordenadas, seguindo a direção das linhas internas desenhadas por Katifori. Dentro do novo polígono interno, as rugas ainda se formam, mas permanecem desordenadas e imprevisíveis.
Tobasco aponta para outro exemplo, que ele determinou ser universalmente verdadeiro para formas cortadas de conchas curvas negativamente. "No final, é muito simples prever os padrões de rugas. Tudo o que você precisa fazer é desenhar segmentos de linha que encontrem o limite em um ângulo reto." Em outras palavras, comece em um ponto dentro da forma e crie uma linha direta até a borda da forma, mas apenas em um ponto onde um ângulo reto se formará.
Isso levou um ano para a equipe entender. "As equações que determinam o layout das rugas são horríveis de resolver, e muitos dos padrões que observamos em nossos experimentos e simulações são bastante complicados", diz Paulsen. "Mas acontece que sob um certo conjunto de condições, você pode prever o layout das rugas com um conjunto simples de regras. Isso significa que agora temos uma maneira rápida e eficiente de projetar padrões de rugas."
"Sua simplicidade é linda e também útil", acrescenta ele, principalmente para superfícies enrugadas que servem a uma função como permitir adesão ou fluxo de fluido.
Katifori menciona exemplos semelhantes. "Digamos que haja umidade ou umidade no ar. A água se comportará de maneira diferente nos vales e nas colinas de uma superfície sulcada", diz ela. "Ao controlar o padrão de rugas, talvez você possa afetar a forma como a água se condensará."
O que vem a seguir Os pesquisadores ainda precisam entender mais sobre essas superfícies texturizadas complexas, como extrair padrões de rugas desordenadas, por que domínios ordenados e desordenados podem coexistir e por que há uma "reciprocidade" ligando conchas curvas negativa e positivamente, ou seja, uma vez que o padrão para um é determinado, é simples prever o padrão para o outro.
Por enquanto, no entanto, eles dizem que estão empolgados com o potencial do que aprenderam até agora.
“Você tem uma teoria complicada que, no final das contas, se resume a matemática relativamente simples que quase qualquer um pode fazer com uma bússola e uma régua”, diz Katifori. "É uma solução elegante e bonita para um problema complexo."
+ Explorar mais Usando provas matemáticas, experimentos e simulações para mostrar como um material enruga quando achatado
