
Neste exemplo, um canto do triângulo está frustrado. Crédito:Johan Jarnestad / The Royal Swedish Academy of Sciences, CC BY-NC
O Prêmio Nobel de Física de 2021 foi concedido em conjunto ao italiano Giorgio Parisi, Syukuro Manabe do Japão e Klaus Hasselmann da Alemanha por suas "contribuições inovadoras para a nossa compreensão de sistemas complexos".
Quando eu ouvi a notícia, Eu mal pude acreditar. Estudei para minha tese de mestrado e meu doutorado. Doutor em física teórica com o professor Parisi na Sapienza University em Roma.
Quando digo que não acreditei, não me entenda mal. De todas as pessoas que conheci em minha experiência de pesquisa - talvez em minha vida - ele é sem dúvida o mais engenhoso. Portanto, não fiquei surpreso com a decisão do comitê do Prêmio Nobel de nomeá-lo como laureado. Em vez, foi a decisão deles de reconhecer suas "contribuições para nossa compreensão de sistemas complexos" que despertou meu interesse.
Este prêmio para o Professor Parisi, dividida com os pioneiros meteorologistas Professor Manabe e Professor Hasselmann, é um reconhecimento incrível de toda uma área de pesquisa - talvez um pouco menos glamorosa do que os gostos da relatividade geral ou da teoria das cordas - que tenta entender e modelar o que nós na física chamamos de "sistemas complexos".
Isso inclui coisas como ecossistemas climáticos, sistemas financeiros, e fenômenos biológicos, para nomear alguns. A grande variedade de sistemas complexos - representados em mercados flutuantes e em bandos de estorninhos - torna muito difícil derivar qualquer tipo de regra universal para eles. O trabalho de Parisi nos permitiu tirar conclusões sem precedentes sobre tais sistemas que, na superfície, parece aleatório, imprevisível e impossível de modelar teoricamente.
Ao contrário de alguns outros modelos de física, sistemas complexos não são uma coleção de partículas idênticas, interagindo regularmente de uma forma consistente e previsível. Em vez de, sistemas complexos são sistemas de elementos, potencialmente diferentes uns dos outros, interagindo de maneiras diferentes e aparentemente imprevisíveis enquanto exposto a diversas condições externas.
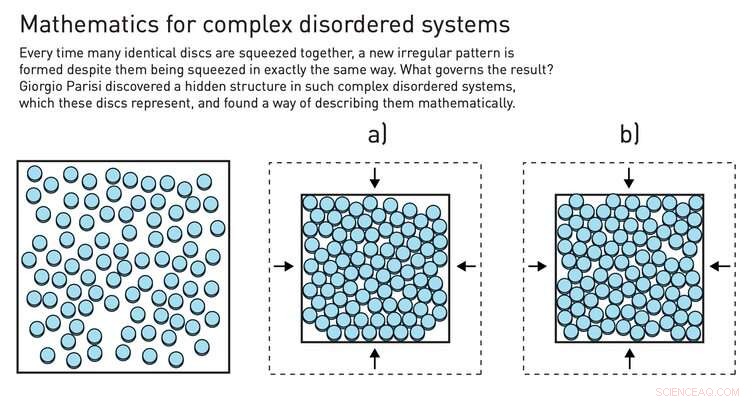
O truque da réplica pode ser realizado comprimindo bolas em uma caixa. Crédito:Johan Jarnestad / The Royal Swedish Academy of Sciences, CC BY-NC
Um trampolim para modelar sistemas complexos é a teoria dos "sistemas desordenados". Estes são essencialmente sistemas em que diferentes pares de elementos experimentam diferentes, forças potencialmente conflitantes que podem levar os elementos a se tornarem "frustrados".
Uma forma de ilustrar isso é imaginar uma festa (um sistema social fechado), onde Alice pode querer conversar com Bob, e Bob pode querer conversar com Charlie, mas Charlie pode não querer conversar com Alice. Há frustração aqui - então o que eles devem fazer?
A pesquisa do professor Parisi esclareceu o que acontece quando a frustração ocorre em sistemas desordenados e complexos. Ele identificou que sistemas complexos são capazes de lembrar suas trajetórias ao longo do tempo, e pode ficar preso em estados abaixo do ideal por um longo tempo.
Em nosso exemplo de festa, imagine Alice, Prumo, Charlie, e outros convidados alterando irregularmente grupos de conversação e parceiros, na esperança de encontrar o melhor grupo de pessoas para conversar, mas potencialmente nunca o encontrando. Esse é o estado sub-ótimo em que os sistemas complexos podem ficar presos.
Padrões de desordem
Uma das muitas ferramentas teóricas que o professor Parisi usou para estabelecer sua teoria é o chamado "truque da réplica" - um método matemático que usa um sistema desordenado, replica várias vezes, e compara como diferentes réplicas do sistema se comportam. Você consegue fazer isso, por exemplo, comprimindo bolas de gude em uma caixa, que formará uma configuração diferente cada vez que você fizer a compressão. Ao longo de muitas repetições, Parisi sabia, padrões reveladores podem surgir.
Este método é agora um dos poucos pilares teóricos para o desenvolvimento de toda a teoria dos sistemas complexos como a conhecemos hoje. A teoria do Professor Parisi demonstrou fornecer previsões confiáveis sobre as propriedades estatísticas de sistemas complexos, desde líquidos super-resfriados (líquidos abaixo de sua temperatura de solidificação), líquidos congelados, sólidos amorfos, como vidro, e até bandos de estorninhos.
A teoria dos sistemas desordenados nos permite entender o belo surgimento de padrões de voo coerentes dentro de bandos compactos de pássaros - que conseguem se manter unidos e formar vastos agrupamentos, apesar das condições adversas.
A mesma estrutura foi usada para dar sentido ao clima da Terra. Os meteorologistas que dividem o prêmio Nobel com o professor Parisi terão contado com avanços na física teórica para produzir os modelos que agora usamos para demonstrar o aquecimento global de forma confiável.
Tive a oportunidade de discutir esses tópicos com o professor Parisi em Roma, durante suas experiências com bandos de pássaros e durante suas simulações de computador sobre o comportamento do vidro. Conhecendo um pouco de sua mente, Não estou nem um pouco surpreso por ele ter recebido o prêmio Nobel de física.
Mas estou agradavelmente surpreso que o campo de sistemas complexos, que está avançando silenciosamente na fronteira da pesquisa teórica em física, recebeu esta exposição. Este prêmio Nobel proporcionou nova legitimidade - e, podemos esperar, novas mentes - para esta área fascinante da física contemporânea.
Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original. 