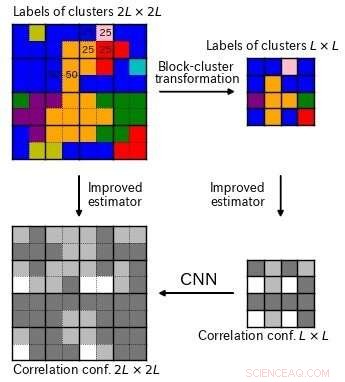
Uma configuração de correlação (canto superior esquerdo) é reduzida usando uma transformação de cluster de bloco recém-desenvolvida (canto superior direito). Ambas as configurações original e reduzida têm uma técnica de estimador aprimorada aplicada para dar pares de configuração de tamanhos diferentes (linha inferior). Usando esses pares de treinamento, uma CNN pode aprender a converter padrões pequenos em grandes, alcançar uma transformação RG inversa bem-sucedida. Crédito:Tokyo Metropolitan University
Pesquisadores da Tokyo Metropolitan University aprimoraram as técnicas de aprendizado de máquina de "super-resolução" para estudar as transições de fase. Eles identificaram as principais características de como grandes matrizes de partículas interagentes se comportam em diferentes temperaturas, simulando minúsculas matrizes antes de usar uma rede neural convolucional para gerar uma boa estimativa de como seria uma matriz maior usando configurações de correlação. A enorme economia em custos computacionais pode proporcionar maneiras únicas de entender como os materiais se comportam.
Estamos rodeados por diferentes estados ou fases da matéria, ou seja, gases, líquidos, e sólidos. O estudo das transições de fase, como uma fase se transforma em outra, está no cerne da nossa compreensão da matéria no universo, e continua sendo um tema quente para os físicos. Em particular, a ideia de universalidade, em que materiais totalmente diferentes se comportam de maneiras semelhantes graças a alguns recursos compartilhados, é poderoso. É por isso que os físicos estudam sistemas modelo, geralmente grades simples de partículas em um array que interagem por meio de regras simples. Esses modelos destilam a essência da física comum compartilhada por materiais e, Surpreendentemente, ainda exibem muitas das propriedades dos materiais reais, como transições de fase. Devido à sua simplicidade elegante, essas regras podem ser codificadas em simulações que nos dizem como os materiais se parecem em diferentes condições.
Contudo, como todas as simulações, o problema começa quando queremos olhar para muitas partículas ao mesmo tempo. O tempo de computação necessário torna-se particularmente proibitivo perto das transições de fase, onde a dinâmica desacelera, e o comprimento da correlação, uma medida de como o estado de um átomo se relaciona com o estado de outro a alguma distância, cresce cada vez mais. Esse é um dilema real se quisermos aplicar essas descobertas ao mundo real:os materiais reais geralmente sempre contêm muito mais ordens de magnitude de átomos e moléculas do que a matéria simulada.
É por isso que uma equipe liderada pelos professores Yutaka Okabe e Hiroyuki Mori da Universidade Metropolitana de Tóquio, em colaboração com pesquisadores do Instituto Shibaura de Tecnologia e Instituto de Bioinformática de Cingapura, têm estudado como extrapolar de forma confiável simulações menores para maiores usando um conceito conhecido como grupo de renormalização inversa (RG). O grupo de renormalização é um conceito fundamental na compreensão das transições de fase e levou Wilson a receber o Prêmio Nobel de Física de 1982. Recentemente, o campo conheceu um poderoso aliado em redes neurais convolucionais (CNN), a mesma ferramenta de aprendizado de máquina ajudando a visão computacional a identificar objetos e decifrar a caligrafia. A ideia seria dar a um algoritmo o estado de uma pequena matriz de partículas e fazer com que ele estimasse a aparência de uma matriz maior. Existe uma forte analogia com a ideia de imagens de super resolução, onde em bloco, imagens pixeladas são usadas para gerar imagens mais suaves em uma resolução mais alta.
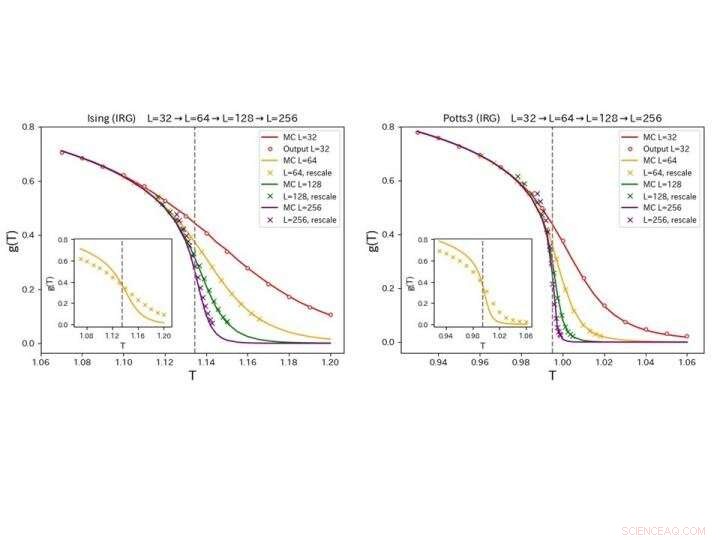
As tendências encontradas em simulações de sistemas maiores são reproduzidas fielmente pelos CNNs treinados para os modelos de Ising (esquerda) e Potts de três estados (direita). (inserção) O reescalonamento correto da temperatura é obtido usando dados em algum tamanho de sistema arbitrário. Crédito:Tokyo Metropolitan University
A equipe tem estudado como isso é aplicado a modelos de spin de matéria, onde as partículas interagem com outras partículas próximas através da direção de seus spins. Tentativas anteriores têm lutado particularmente para aplicar isso a sistemas em temperaturas acima de uma transição de fase, onde as configurações tendem a parecer mais aleatórias. Agora, em vez de usar configurações de rotação, ou seja, instantâneos simples de qual direção as partículas de rotação estão apontando, eles consideraram configurações de correlação, onde cada partícula é caracterizada por quão semelhante seu próprio spin é ao de outras partículas, especificamente aqueles que estão muito distantes. Acontece que as configurações de correlação contêm filas mais sutis sobre como as partículas são organizadas, particularmente em temperaturas mais altas.
Como todas as técnicas de aprendizado de máquina, a chave é ser capaz de gerar um conjunto de treinamento confiável. A equipe desenvolveu um novo algoritmo chamado de transformação de cluster de bloco para configurações de correlação para reduzi-las a padrões menores. Aplicando uma técnica de estimador aprimorada aos padrões original e reduzido, eles tinham pares de configurações de tamanhos diferentes com base nas mesmas informações. Tudo o que resta é treinar a CNN para converter os padrões pequenos em padrões maiores.
O grupo considerou dois sistemas, o modelo de Ising 2D e o modelo de Potts de três estados, ambos os principais benchmarks para estudos de matéria condensada. Para ambos, eles descobriram que sua CNN poderia usar uma simulação de um conjunto muito pequeno de pontos para reproduzir como uma medida da correlação g (T) mudou em um ponto de transição de fase em sistemas muito maiores. Comparando com simulações diretas de sistemas maiores, as mesmas tendências foram reproduzidas para ambos os sistemas, combinado com um reescalonamento de temperatura simples com base em dados em um tamanho de sistema arbitrário.
Uma implementação bem-sucedida de transformações RG inversas promete dar aos cientistas um vislumbre de tamanhos de sistema anteriormente inacessíveis, e ajudar os físicos a compreender as características de grande escala dos materiais. A equipe agora espera aplicar seu método a outros modelos que podem mapear recursos mais complexos, como uma faixa contínua de giros, bem como o estudo de sistemas quânticos.