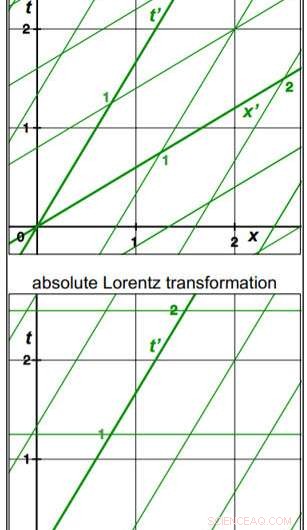
Crédito:World Scientific Publishing
Um dos aspectos estruturais mais básicos do espaço-tempo relativístico é a descrição de como o tempo e as distâncias são alterados pelo movimento. A teoria da relatividade especial descreve uma estrutura do espaço-tempo para movimento constante linear em que o tempo se dilata e os comprimentos se contraem em resposta ao movimento. Esta estrutura é descrita pela transformação de Lorentz, que engloba fórmulas matemáticas que descrevem como o tempo e a distância são alterados entre os referenciais em movimento. A transformação de Lorentz também descreve como um observador estacionário visualiza o tempo no quadro móvel para ser compensado com a distância. A compensação do tempo com a distância entre os quadros de referência gera simultaneidade diferencial, em que eventos que são simultâneos para um observador não serão simultâneos para um segundo observador se movendo em relação ao primeiro observador.
A natureza do espaço-tempo em quadros rotativos não foi estabelecida no nível mais fundamental de definição da transformação que descreve com precisão os efeitos relativísticos e a estrutura de simultaneidade. Existem quatro transformações relativísticas rotacionais distintas na literatura:a métrica de Langevin; Pós-transformação; Transformação de Franklin; e a transformação de Lorentz absoluta (ALT) em sua forma rotacional. Determinar qual transformação descreve com precisão os dados experimentais indicaria a estrutura do espaço-tempo que está presente em estruturas rotativas do mundo real. A compreensão desta informação fundamental tem ampla aplicabilidade porque a maioria da matéria visível no Universo está em movimento rotacional, incluindo a rotação da Terra.
A transformação rotacional mais amplamente citada é a métrica Langevin, que foi descrito pela primeira vez em 1921. Ao longo das décadas, a métrica Langevin foi usada para descrever a relatividade em quadros rotativos em centenas de livros e artigos de pesquisa. Contudo, a métrica Langevin nunca foi avaliada com dados experimentais que tenham resolução suficiente para distingui-la das outras grandes transformações rotacionais.
A combinação de efeitos relativísticos e estrutura de simultaneidade de uma transformação afeta como a luz se propaga. As quatro transformações têm diferentes previsões para as velocidades unidirecionais da luz, velocidade da luz nos dois sentidos, e o efeito Sagnac. Este estudo deriva as previsões ópticas para cada transformação diretamente de suas equações de transformação, com várias das previsões não relatadas anteriormente na literatura. As previsões são então comparadas com dados experimentais ópticos de alta resolução recentes.
Os dados do ressonador óptico na velocidade bidirecional da luz estão entre as medições científicas de mais alta resolução, com resoluções de 10 -18 . Essa alta resolução é necessária para distinguir entre as previsões das transformações. O estudo revela que ALT e a previsão de transformação de Franklin da velocidade constante de duas vias da luz, c, corresponde aos dados do ressonador óptico, enquanto a métrica Langevin e as previsões de pós-transformação são invalidadas pelos dados. A falha da métrica Langevin e da transformação Post para coincidir com os dados do ressonador óptico é mostrada como sendo devido à sua nenhuma (ou nenhuma) contração de comprimento total na estrutura rotativa. Em contraste, as transformações ALT e Franklin exibem contração de comprimento, o que permite suas previsões precisas para a velocidade bidirecional da luz.
Dados sobre o efeito Sagnac, que tem resoluções menores de 10 -8 , é compatível com as previsões do efeito Sagnac da métrica Langevin, Publicar, e transformações ALT, mas é incompatível com a transformação de Franklin, que não prevê nenhum efeito Sagnac. O fracasso da transformação de Franklin em gerar um efeito Sagnac evidente é devido à incorporação de simultaneidade diferencial. Em contraste, as outras três transformações incorporam simultaneidade absoluta em que o tempo não é compensado com a distância, que permite efeitos Sagnac evidentes. Assim, ALT é a única transformação que descreve com precisão toda a gama de dados ópticos relativísticos.
Múltiplas publicações propuseram mecanismos para incorporar simultaneidade diferencial em quadros rotativos para permitir a geração de um efeito Sagnac evidente. Contudo, esses mecanismos geram equações de efeito Sagnac alternativas. O estudo mostra que essas equações de efeito Sagnac alternativas implicam velocidades bidirecionais da luz que são invalidadas pelos dados do ressonador óptico de alta resolução. Em contraste, ALT prevê o efeito Sagnac convencional, o que implica a velocidade constante de duas vias da luz, c.
O estudo demonstra que a transformação rotacional ALT prediz com precisão dados ópticos de alta resolução e observações relativísticas não ópticas de quadro rotativo. Esta análise implica que a transformação rotacional ALT descreve a estrutura básica do espaço-tempo em estruturas rotativas. Isso esclarece que o espaço-tempo de quadro rotativo é caracterizado pelos efeitos relativísticos da dilatação do tempo e da contração do comprimento dentro de uma estrutura de simultaneidade absoluta na qual o tempo não é compensado pela distância.