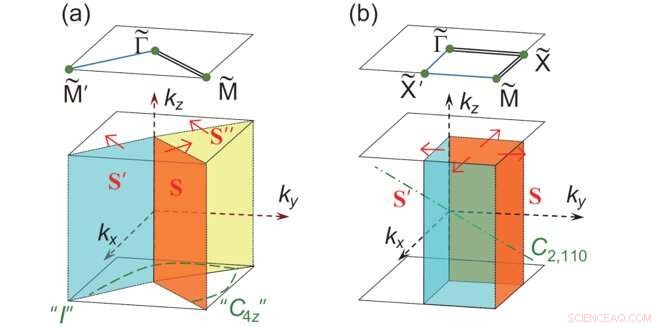
A definição de χ em sistemas com simetria S4 na superfície laranja S. O sistema em (b) tem C2, 110 simetria. Crédito:Science China Press
Um novo invariante topológico χ é definido em sistemas com S 4 simetria para diagnosticar a existência de férmions de Weyl. Calculando χ, o custo computacional para pesquisar semimetais de Weyl é bastante reduzido. Recentemente, Gao et al. implementou este método na triagem de alto rendimento e encontrou muitos novos candidatos de semimetal de Weyl com propriedades exóticas, fornecendo plataformas realistas para futuros estudos experimentais da interação entre os férmions de Weyl e outros estados exóticos.
Usando as simetrias dos sistemas, as pessoas podem definir vários invariantes topológicos para descrever diferentes estados topológicos. Os materiais topológicos podem ser descobertos com precisão calculando os invariantes topológicos. Recentemente, pesquisadores descobriram que representações irredutíveis e relações de compatibilidade podem ser usadas para determinar se um material é um isolante topológico não trivial / trivial (satisfazendo as relações de compatibilidade) ou semimetal topológico (violando as relações de compatibilidade), o que leva a um grande número de materiais topológicos previstos por cálculos teóricos.
Contudo, Os semimetais de Weyl vão além deste paradigma porque a existência de férmions de Weyl não precisa de nenhuma proteção de simetria (exceto para simetrias de translação de rede). Atualmente, as pessoas geralmente pegam uma grade muito densa na zona tridimensional de Brillouin para procurar férmions de Weyl com zero banda gap. Devido à grande quantidade de computação necessária, este método é muito ineficiente. Portanto, não pode ser usado para pesquisa de alto rendimento para férmions de Wey. Considerando o enorme potencial de aplicações dos semimetais de Weyl, é urgente projetar um novo algoritmo ou definir um novo invariante topológico para pesquisar férmions de Weyl com precisão e rapidez.
Em um trabalho recente publicado em Boletim de Ciências , Gao et al. propôs um novo invariante topológico χ em sistemas com S 4 simetria, que pode ser usado para diagnosticar a existência de férmions de Weyl de forma eficaz. Além disso, para sistemas magnéticos, o diferente de zero χ pode ser revelado pelas representações irredutíveis de estados ocupados em S 4 pontos k invariantes. Assim, ele reduz muito o custo de cálculo para procurar fermions de Weyl. É importante notar que este novo χ invariante funciona para sistemas magnéticos e não magnéticos.
Ao aplicar este método à triagem de alto rendimento nos cálculos dos primeiros princípios, os autores previram muitos novos semimetais Weyl magnéticos e não magnéticos. As observações experimentais mostraram que esses semimetais de Weyl recém-descobertos possuem muitas propriedades únicas, como magnetorresistência, supercondutividade, e spin glassy states etc. Esses materiais fornecem plataformas realistas para futuros estudos experimentais da interação entre os férmions de Weyl e outros estados exóticos.