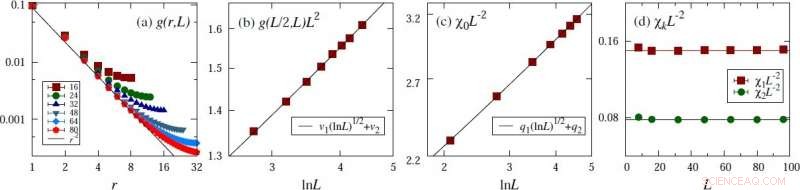
Evidência para a forma de escala conjecturada no exemplo do modelo 4D XY crítico. (a) Função de correlação de dois pontos. (b) Correlação de dois pontos na distância da metade do tamanho do sistema linear. (c) Suscetibilidade magnética. (d) Flutuações magnéticas em modos Fourier diferentes de zero. Crédito:© Science China Press
Desde o estabelecimento da teoria do grupo de renormalização, sabe-se que os sistemas de fenômenos críticos normalmente possuem uma dimensão crítica superior dc (dc =4 para o modelo O (n)), de modo que em dimensões espaciais iguais ou superiores a dc, o comportamento termodinâmico é governado por expoentes críticos tomando valores de campo médio. Em contraste com a simplicidade do comportamento termodinâmico, a teoria da escala de tamanho finito (FSS) para d> O modelo dc O (n) era surpreendentemente sutil e permaneceu sujeito a um debate contínuo até recentemente, quando um ansatz de escala de dois comprimentos para a função de correlação de dois pontos foi conjecturado, confirmado numericamente, e parcialmente apoiado por cálculos analíticos.
Na dimensionalidade crítica superior dc, correções logarítmicas multiplicativas e aditivas geralmente ocorrem no comportamento do campo médio puro. O esclarecimento das correções logarítmicas no FSS torna-se 'notoriamente difícil, 'devido à falta de percepções analíticas além do nível fenomenológico e do limite de tamanhos de sistema disponíveis em simulações numéricas. A forma FSS logarítmica precisa em d =dc continua sendo um problema de longa data.
Recentemente, Jian-Ping Lv, Wanwan Xu, e Yanan Sun da Universidade Normal de Anhui, Kun Chen da Rutgers, a State University of New Jersey, e Youjin Deng da Universidade de Ciência e Tecnologia da China e da Universidade de Minjiang abordaram o FSS logarítmico da simetria O (n) na dimensionalidade crítica superior. Emprestando insights de dimensões superiores, eles estabeleceram uma forma de escala explícita para a densidade de energia livre, que consiste simultaneamente em um termo de escala para o ponto fixo gaussiano e outro termo com correções logarítmicas multiplicativas. Em particular, eles conjeturaram que a correlação crítica de dois pontos de tamanho finito exibe um comportamento de dois comprimentos, que é governado pelo ponto fixo gaussiano a uma distância mais curta, e entra em um platô a uma distância maior, cuja altura diminui com o tamanho do sistema em uma lei de potência corrigida por um expoente logarítmico.
Nesta base, o FSS de várias quantidades macroscópicas foram previstas. Eles então realizaram simulações de Monte Carlo extensas para o modelo de n-vetor com n =1, 2, 3, e obteve evidências sólidas que apoiam as formas de escalonamento conjecturadas do FSS da suscetibilidade, as flutuações magnéticas em modos diferentes de zero de Fourier, o cumulante Binder, bem como a correlação de dois pontos na distância da metade do tamanho do sistema linear. Este é um passo significativo em direção a uma solução completa do FSS logarítmico em d =dc para sistemas com uma dimensionalidade crítica superior.
O estudo não é apenas de importância teórica em sistemas modelo, mas também de relevância prática para um grande número de sistemas experimentais. Observa-se que devido aos desenvolvimentos tecnológicos, a realização experimental do modelo O (n) está agora disponível em vários sistemas físicos, incluindo materiais magnéticos quânticos, Matrizes de junção Josephson, e sistemas atômicos ultracold. De acordo com o mapeamento quântico-clássico, os sistemas quânticos tridimensionais O (n) estão na dimensionalidade crítica superior.