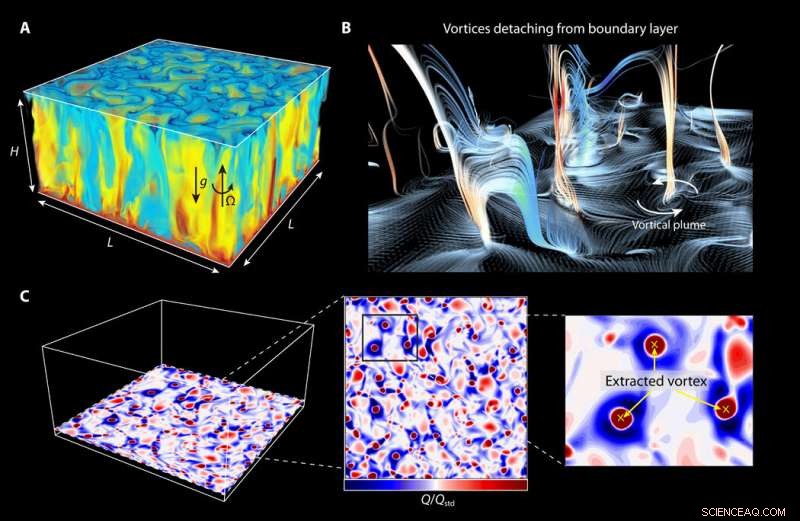
Estruturas de fluxo com rotação. Instantâneos de (A) as linhas de temperatura θ e (B) originadas da camada limite térmica inferior. (C) Instantâneos de Q / Qstd (critério Q) tirados horizontalmente na borda da camada limite térmica para o número de Ekman (Ek) =4 × 10−5 e Ra =108 e uma demonstração do vórtice extraído. As localizações do centro do vórtice são marcadas como cruzes amarelas. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110
O movimento browniano de partículas em fluido é um comportamento coletivo comum em sistemas biológicos e físicos. Em um novo relatório sobre Avanços da Ciência , Kai Leong Chong, e uma equipe de pesquisadores em física, Engenharia, e engenharia aeroespacial na China, conduziu experimentos e simulações numéricas para mostrar como o movimento dos vórtices se assemelhava às partículas brownianas inerciais. Durante os experimentos, o fluxo vortical convectivo turbulento em rotação permitiu que as partículas se movessem balisticamente no início e difusivamente após um momento crítico em uma transição comportamental direta - sem passar por um regime de memória hidrodinâmica. O trabalho implica que vórtices convectivos têm memória induzida por inércia, portanto, seu movimento de curto prazo foi bem definido na estrutura do movimento browniano aqui pela primeira vez.
movimento browniano
Albert Einstein forneceu pela primeira vez uma explicação teórica para o movimento browniano em 1905 com o movimento das partículas de pólen em um banho termal, o fenômeno agora é um exemplo comum de processos estocásticos que ocorrem amplamente na natureza. Mais tarde, em 1908, Paul Langevin notou a inércia das partículas e previu que seu movimento seria balístico em um curto período de tempo, mudando para movimento difuso após uma linha do tempo específica. Contudo, devido à rapidez desta transição, levou mais de um século para que os pesquisadores pudessem observar diretamente o fenômeno. No entanto, o movimento browniano "puro" previsto por Langevin não foi observado em sistemas líquidos e a transição abrangeu uma ampla gama de escalas de tempo. A transição lenta e suave ocorreu devido ao efeito de memória hidrodinâmica, para gerar correlações de longo alcance. Os cientistas já haviam observado o efeito da memória hidrodinâmica em vários sistemas, incluindo suspensões coloidais, partículas suspensas no ar e partículas presas em pinças ópticas. Nesse trabalho, Chong et al. mostrou como vórtices em fluxos altamente conectivos se comportavam como partículas inerciais para realizar o movimento browniano puro, pela primeira vez, sem ser influenciado pelo efeito hidrodinâmico. Eles identificaram e extraíram os vórtices usando o critério Q (um método para identificação de vórtices). O trabalho os ajudará a prever o movimento do vórtice durante um período específico de tempo em sistemas astrofísicos e geofísicos.
Movimento balístico a difusivo de vórtices convectivos. (A) O MSD dos vórtices em função do tempo. (B) MSD normalizado em função de t / tc. A linha sólida representa um ajuste da Eq. 4 para os dados. Em (A) e (B), símbolos sólidos denotam resultados numéricos em Ra =1 × 108, e os símbolos abertos denotam resultados experimentais em Ra =3 × 107. (C) Coeficiente de difusão D de vórtices (símbolos abertos) e a escala de tempo característica tc para transição de movimento (símbolos sólidos) como uma função Ra / Rac. (D) Função de autocorrelação de velocidade (VACF) versus t / tc para diferentes Ek. A linha tracejada representa C (t) =2Dtcexp (−t / tc). A linha contínua indica uma queda da lei de potência para o VACF (os dados para t ≳ 5tc têm alguma dispersão devido a estatísticas insuficientes). Observe que todas as grandezas físicas são adimensionais, conforme descrito no texto principal. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110 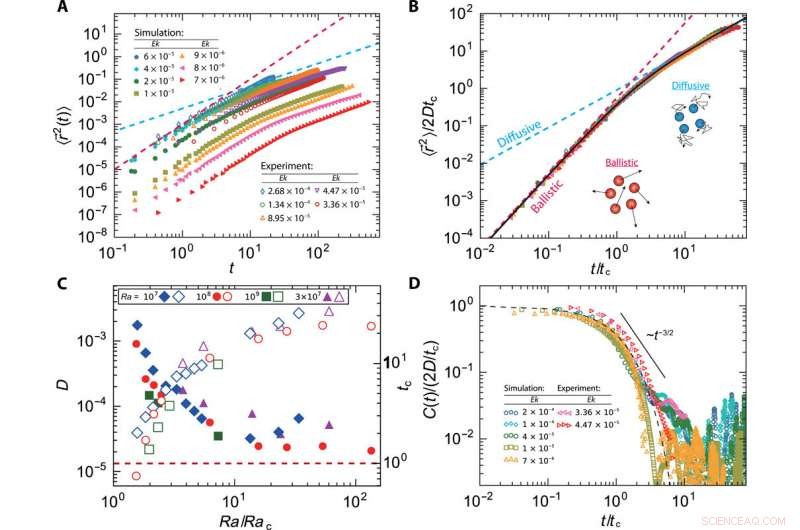
Um desafio existente na pesquisa astrofísica e geofísica é prever o movimento dos vórtices dentro de um período de tempo específico. Chong et al. usou um sistema de modelo para estudar vórtices em fluxos convectivos conhecido como convecção Rayleigh Benard (RB), que inclui uma camada de fluido de altura fixa, aquecido por baixo e resfriado por cima, enquanto é girado em torno do eixo vertical a uma velocidade angular. A diferença de temperatura no sistema desestabilizou o fluxo para que a convecção ocorresse quando o acionamento térmico fosse suficientemente forte. Os cientistas usaram três parâmetros adimensionais para caracterizar a dinâmica do fluxo, incluindo o número de Rayleigh (Ra), Número de Prandtl (Pr) e o número de Ekman (Ek). Na presença de rotação, estruturas vorticais emergiram como pacotes de fluido em espiral para cima ou para baixo. Os pesquisadores continuam a investigar essas plumas vorticais devido à sua importância no momento e no transporte de calor.
Chong et al. primeiro estudou o movimento dos vórtices rastreando sua mudança de posição por meio de uma série de instantâneos. Eles caracterizaram o comportamento estatístico dos vórtices usando seu deslocamento quadrático médio (MSD). Os valores de MSD para diferentes Ek e Ra exibiram comportamento semelhante, indicando que em um curto espaço de tempo o movimento do vórtice foi transferido do movimento balístico para o movimento difusivo. Essa transição lembrava o movimento browniano em um banho termal. Os cientistas, portanto, trataram os vórtices como partículas brownianas e descreveram seu movimento resolvendo a equação de Langevin para obter seu MSD. Os resultados implicaram dinâmica semelhante de movimento de vórtice para Ra e Ek, sugerindo que os vórtices exibiam comportamento "browniano puro". No sistema de convecção, os vórtices carregavam pacotes de fluido que eram mais quentes e mais frios do que o fluido circundante; esta diferença de densidade relativamente pequena causada por variações de temperatura no experimento deu origem ao notável comportamento balístico.
Vórtices formando um padrão semelhante a uma rede com taxa de rotação alta o suficiente. (A) Instantâneos de Q / Qstd tirados horizontalmente na borda da camada limite térmica para, da esquerda para a direita, Ek =4 × 10−5, 1 × 10−5, e 7 × 10−6 em Ra =108. (B) Função de distribuição radial g (r) como uma função de r / a, onde a é o raio médio dos vórtices. (C) O valor máximo gmax da função de distribuição radial versus Ra / Rac (o caso de Ra =3 × 107 é do experimento, os outros são do DNS). Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110 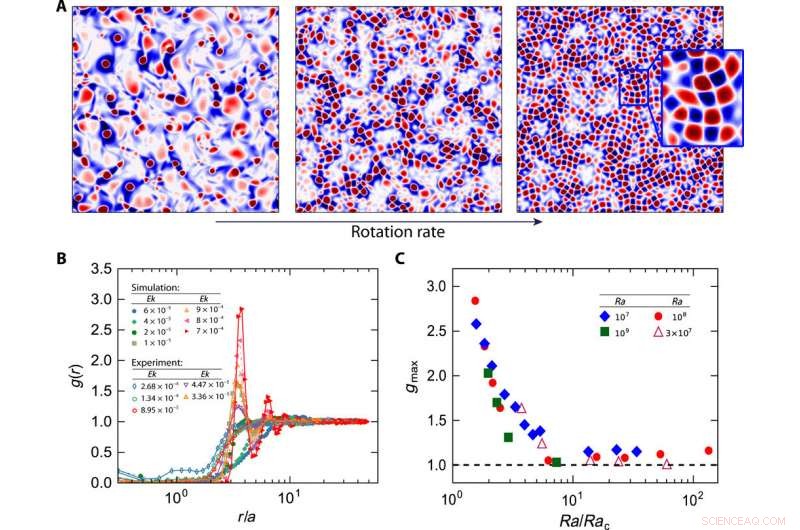
Apesar do movimento browniano, a distribuição espacial dos vórtices não era aleatória, e exibiu estruturas padronizadas, que os cientistas obtiveram usando instantâneos de várias taxas de rotação. Como o número Ekman (Ek) variou, várias mudanças ocorreram na distribuição do vórtice. Inicialmente, o número de vórtices aumentou com a taxa de rotação, de modo que os vórtices inicialmente diluídos e distribuídos aleatoriamente tornaram-se altamente concentrados e agrupados. O aumento da densidade do número de vórtices com a taxa de rotação também concordou com as investigações anteriores. Próximo, quando a taxa de rotação tornou-se suficientemente alta, eles formaram uma estrutura de grade de vórtice. Quando Chong et al. ampliado em uma região local para observar a maior taxa de rotação, eles observaram um padrão regular para tais estruturas de grade de vórtice. As regiões avermelhadas dos vórtices formaram uma rede quadrada e as regiões azuladas localizadas intermediárias mostraram comportamento de alta tensão. A equipe creditou os padrões de quadratura observados no trabalho a diferentes configurações de limites e parâmetros de controle.
Apesar do movimento aleatório no domínio temporal, os vórtices mostraram uma ordem espacial específica, o que resultou em uma aparente contradição. Chong et al. observou as trajetórias dos vórtices durante a rotação lenta e rápida. Contudo, os vórtices não viajaram longe o suficiente para "ver" ou interagir com outros vórtices. Eles creditaram a ordem espacial dos vórtices à competição entre os dois processos dinâmicos caracterizados pela escala de tempo de relaxamento do vórtice e escala de tempo browniana, respectivamente.
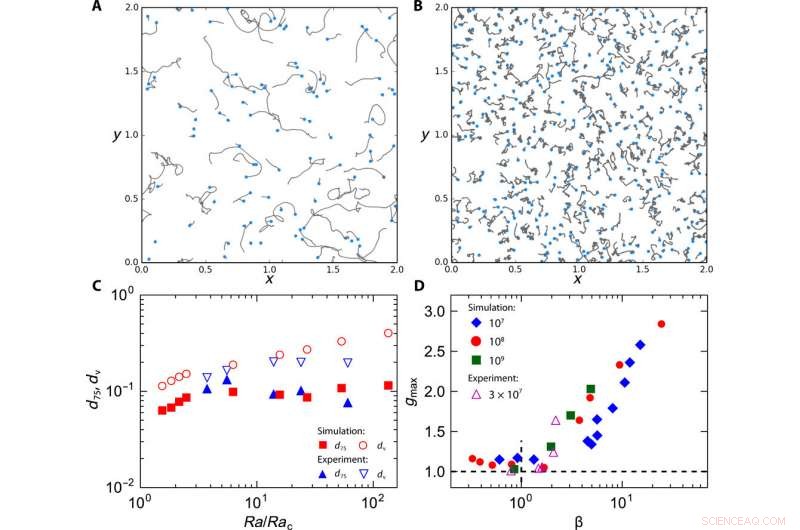
Movimento localizado de vórtices. Trajetórias de vórtices:(A) Ek =1 × 10−4 e (B) Ek =7 × 10−6; em ambos os casos, Ra =1 × 108. Os pontos azuis indicam o fim das trajetórias. (C) A separação média (dv) entre vórtices (símbolos abertos) e o 75º percentil da distância (d75) percorrida por vórtices (símbolos sólidos), como uma função de Ra / Rac para Ra =1 × 108 (simulação, símbolos vermelhos) e Ra =3 × 107 (experimento, símbolos azuis). (D) A função de distribuição radial máxima gmax versus β definida como a razão entre a escala de tempo browniana e a escala de tempo de relaxamento. Crédito:Science Advances, doi:10.1126 / sciadv.aaz1110
Desta maneira, Kai Leong Chong e colegas mostraram como o movimento dos vórtices na convecção térmica rotativa se assemelhava a partículas inerciais realizando o movimento browniano. O movimento passou por uma transição brusca de regiões balísticas para difusivas sem experimentar uma região de memória hidrodinâmica intermediária. A observação do movimento browniano puro foi prevista pela primeira vez por Paul Langevin, embora não tenha sido observado anteriormente na prática para partículas inerciais em sistemas líquidos. O trabalho destacou o trabalho teórico clássico existente que mostrou como os traços passivos exibiram uma transição do comportamento balístico para o difusivo, semelhantes às observações experimentais deste estudo. O movimento browniano puro observado também indicou a insignificância do efeito da memória hidrodinâmica. Chong et al. considerou a força de Coriolis durante o estudo devido à sua relevância na formação de vórtices em fenômenos naturais, incluindo ciclones tropicais na atmosfera, vórtices oceânicos e a mancha vermelha gigante de longa duração em Júpiter. As descobertas irão influenciar muitas situações na astrofísica, geofísica e meteorologia.
© 2020 Science X Network