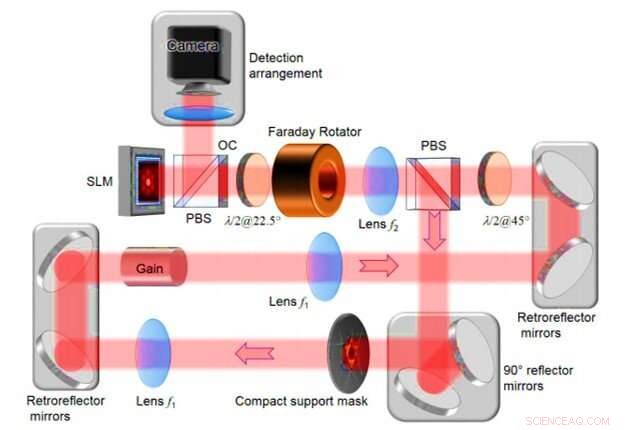
 p Disposição experimental detalhada do laser da cavidade degenerada do anel digital. SLM - modulador de luz espacial; PBS - divisor de feixe de polarização; λ/2@22.5° - placa de meia onda com orientação angular de 22,5 °; λ / 2 @ 45 ° - placa de meia onda com orientação angular de 45 °; máscara de suporte compacto - abertura intracavitária no plano de Fourier; Acoplador de saída OC. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Disposição experimental detalhada do laser da cavidade degenerada do anel digital. SLM - modulador de luz espacial; PBS - divisor de feixe de polarização; λ/2@22.5° - placa de meia onda com orientação angular de 22,5 °; λ / 2 @ 45 ° - placa de meia onda com orientação angular de 45 °; máscara de suporte compacto - abertura intracavitária no plano de Fourier; Acoplador de saída OC. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Os físicos podem explorar sistemas físicos sob medida para resolver rapidamente tarefas computacionais desafiadoras, desenvolvendo simuladores de spin, otimização combinatória e foco de luz através de meios de espalhamento. Em um novo relatório sobre
Avanços da Ciência , C. Tradonsky e um grupo de pesquisadores dos Departamentos de Física em Israel e na Índia abordaram o problema de recuperação de fase reconstruindo um objeto a partir de sua distribuição de intensidade dispersa. O processo experimental abordou um problema existente em disciplinas que vão desde imagens de raios-X à astrofísica que carecem de técnicas para reconstruir um objeto de interesse, onde os cientistas normalmente usam algoritmos iterativos indiretos que são inerentemente lentos. p Na nova abordagem óptica, Tradonsky et al, por outro lado, usaram um modo digital de laser de cavidade degenerada (DDCL) para reconstruir de forma rápida e eficiente o objeto de interesse. Os resultados experimentais sugeriram que a competição de ganho entre os vários modos de laser atuou como um computador altamente paralelo para dissolver rapidamente o problema de recuperação de fase. A abordagem se aplica a objetos bidimensionais (2-D) com suporte compacto conhecido e objetos de valor complexo, para generalizar a imagem por meio de mídia de espalhamento, enquanto realiza outras tarefas computacionais desafiadoras.
p Para calcular a distribuição de intensidade da luz espalhada longe de um objeto desconhecido com relativa facilidade, os pesquisadores podem calcular a fonte do valor absoluto da transformada de Fourier de um objeto. A reconstrução de um objeto a partir de sua distribuição de intensidade espalhada é, Contudo, mal posado, uma vez que as informações de fase podem ser perdidas e distribuições de fases diversas no trabalho podem resultar em reconstruções diferentes. Os cientistas devem, portanto, obter informações prévias sobre a forma de um objeto, positividade, simetria espacial ou dispersão para reconstruções de objetos mais precisas. Esses exemplos são encontrados na astronomia, estudos de caracterização de pulso curto, Difração de raios-X, detecção de radar, reconhecimento de fala e ao gerar imagens em mídias turvas. Durante a reconstrução de objetos com extensão finita (suporte compacto), pesquisadores oferecem uma solução única para o problema de recuperação de fase, contanto que modelem a mesma intensidade espalhada em uma resolução suficientemente maior.
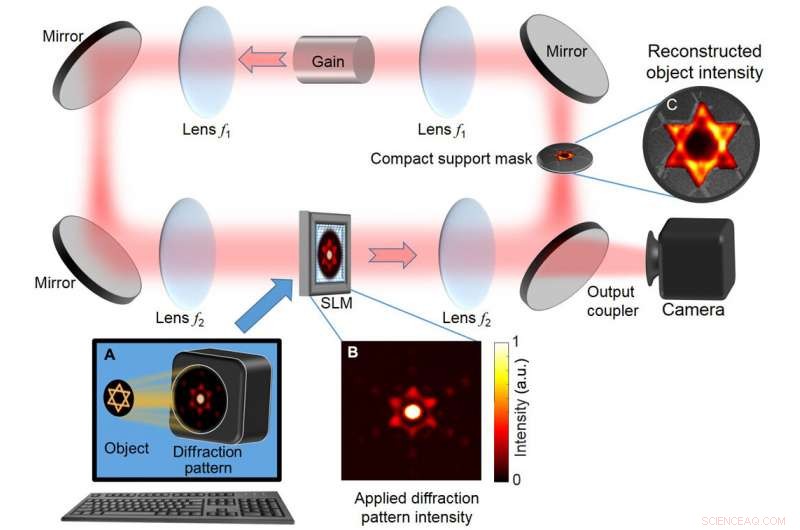 p Arranjo DDCL básico para recuperação rápida de fase. (A) A distribuição de intensidade dispersa calculada do objeto (essencialmente a distribuição de intensidade de Fourier) é aplicada em um SLM, que é incorporado a um laser de cavidade degenerada em anel que pode suportar até 100, 000 modos transversais degenerados. Uma máscara com a forma dos limites do objeto (suporte compacto) no plano de Fourier filtra modos estranhos que não correspondem ao suporte compacto. Com este arranjo de laser, o processo de laser produz uma solução autoconsistente que satisfaz tanto a distribuição de intensidade espalhada mostrada em (B) quanto a restrição de suporte compacto. (C) A intensidade do objeto reconstruído aparece na máscara de suporte compacto e é fotografada na câmera. a.u., unidades arbitrárias. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Arranjo DDCL básico para recuperação rápida de fase. (A) A distribuição de intensidade dispersa calculada do objeto (essencialmente a distribuição de intensidade de Fourier) é aplicada em um SLM, que é incorporado a um laser de cavidade degenerada em anel que pode suportar até 100, 000 modos transversais degenerados. Uma máscara com a forma dos limites do objeto (suporte compacto) no plano de Fourier filtra modos estranhos que não correspondem ao suporte compacto. Com este arranjo de laser, o processo de laser produz uma solução autoconsistente que satisfaz tanto a distribuição de intensidade espalhada mostrada em (B) quanto a restrição de suporte compacto. (C) A intensidade do objeto reconstruído aparece na máscara de suporte compacto e é fotografada na câmera. a.u., unidades arbitrárias. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Os físicos desenvolveram vários algoritmos para resolver o problema de recuperação de fase na última década, incluindo o algoritmo de redução de erro Gerchberg-Saxton (GS), algoritmo híbrido de entrada-entrada e reflexões alternadas médias relaxadas (RAAR). Contudo, eles são baseados em projeções iterativas que são relativamente lentas, mesmo em computadores de alto desempenho. Como uma alternativa, equipes de pesquisa podem enfrentar desafios computacionais usando sistemas físicos especificamente adaptados. Embora tais sistemas não sejam máquinas de Turing universais (ou seja, eles não podem realizar cálculos arbitrários), eles podem potencialmente resolver uma classe específica de problemas com eficiência. Resolver problemas difíceis com tais sistemas pode ser vantajoso em comparação com o uso de computadores convencionais.
p Tradonsky et al demonstraram experimentalmente um novo sistema óptico para resolver rapidamente problemas de recuperação de fase com base em um laser digital de cavidade degenerada (DDCL). O dispositivo incorporou duas restrições, incluindo as magnitudes de Fourier de luz espalhada de um objeto e o suporte compacto. O processo de laser não linear dentro da cavidade resultou em uma solução autoconsistente que atendeu a ambas as restrições. O mecanismo físico subjacente no DDCL foi semelhante ao observado com os estimuladores de rotação do oscilador paramétrico óptico (OPO).
p Ambos os simuladores OPO e DDCLs realizaram otimizações por meio de operação extremamente rápida com capacidade de evitar mínimos locais e possuíam um pacote de ondas não gaussiano. Os cientistas facilitaram a abertura de suporte compacto dentro da cavidade para garantir diferentes configurações de fases do laser para resultar em diferentes perdas, para permitir a configuração com perdas mínimas para vencer a competição de modo e resolver o problema de fase. O sistema DDCL continha muitos recursos atraentes e importantes, incluindo alto paralelismo para fornecer milhões de realizações experimentais paralelas, tempos curtos de ida e volta aproximando-se de 20 nanossegundos, tempos de convergência rápidos e um modo de seleção inerente que contabilizou perdas mínimas devido à competição de modo. Em teoria, de todas as configurações de fase que evoluem com o tempo, aquele com a energia mais alta venceu a competição de modo em relação ao ganho limitado. Como resultado, maior o número de configurações independentes iniciais na prática, maior a probabilidade do sistema encontrar uma solução correta com uma configuração estável e sem perdas.
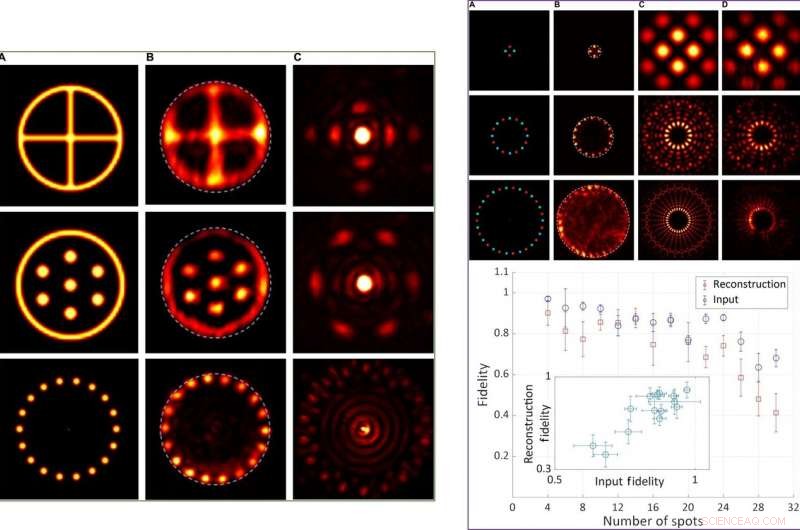 p ESQUERDA:Resultados experimentais para objetos centrossimétricos de valor real. Coluna (A) Distribuições de intensidade dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuições de intensidade de Fourier no SLM. À DIREITA:Resultados experimentais e quantitativos para fidelidade em função da complexidade do objeto. Topo:Distribuições de intensidade representativas de objetos com 4, 16, e 30 pontos. Coluna (A) Distribuições de intensidade (brilho) e fase (matiz) dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuições de intensidade de Fourier calculadas aplicadas para controlar o SLM. Coluna (D) Detectada distribuições de intensidade de Fourier correspondentes após modificações por propriedades SLM. Abaixo:Valores de fidelidade quantitativos das distribuições de intensidade de Fourier (azul) e as distribuições de intensidade do objeto reconstruído (vermelho) em função do número de pontos no objeto (4 a 30). Detalhe:valores de fidelidade das distribuições de intensidade do objeto reconstruído como uma função dos valores de fidelidade das distribuições de intensidade de Fourier para todas as medições. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
p ESQUERDA:Resultados experimentais para objetos centrossimétricos de valor real. Coluna (A) Distribuições de intensidade dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuições de intensidade de Fourier no SLM. À DIREITA:Resultados experimentais e quantitativos para fidelidade em função da complexidade do objeto. Topo:Distribuições de intensidade representativas de objetos com 4, 16, e 30 pontos. Coluna (A) Distribuições de intensidade (brilho) e fase (matiz) dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuições de intensidade de Fourier calculadas aplicadas para controlar o SLM. Coluna (D) Detectada distribuições de intensidade de Fourier correspondentes após modificações por propriedades SLM. Abaixo:Valores de fidelidade quantitativos das distribuições de intensidade de Fourier (azul) e as distribuições de intensidade do objeto reconstruído (vermelho) em função do número de pontos no objeto (4 a 30). Detalhe:valores de fidelidade das distribuições de intensidade do objeto reconstruído como uma função dos valores de fidelidade das distribuições de intensidade de Fourier para todas as medições. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
p Na configuração experimental, Tradonsky et al incluíram um laser de cavidade degenerada em anel com um meio de ganho inerente, dois telescópios 4f e um modulador de luz espacial de amplitude (SLM). O sistema também incluiu uma abertura intracavitária, Espelhos de refletividade 3D e um acoplador de saída. A equipe usou os telescópios 4f da esquerda para criar imagens do centro do meio de ganho no SLM e controlou a transmissão em cada pixel, independentemente. Eles combinaram a abertura intracavitária com o SLM para controlar e formar a distribuição da intensidade do laser de saída. Quando os cientistas colocaram uma abertura intracavitária (máscara de suporte compacta) no plano de Fourier entre as duas lentes, cada distribuição de fase demonstrou um nível diferente de perda. Consequentemente, a distribuição de fase com perda mínima foi o modo de laser mais provável no estudo. A equipe considerou duas figuras de mérito para quantificar a qualidade do sistema, incluindo fidelidade da solução e tempo de computação. A equipe de pesquisa obteve resultados representativos para objetos centrossimétricos com uma concordância muito boa entre as distribuições de intensidade do original (objeto real) e formas reconstruídas.
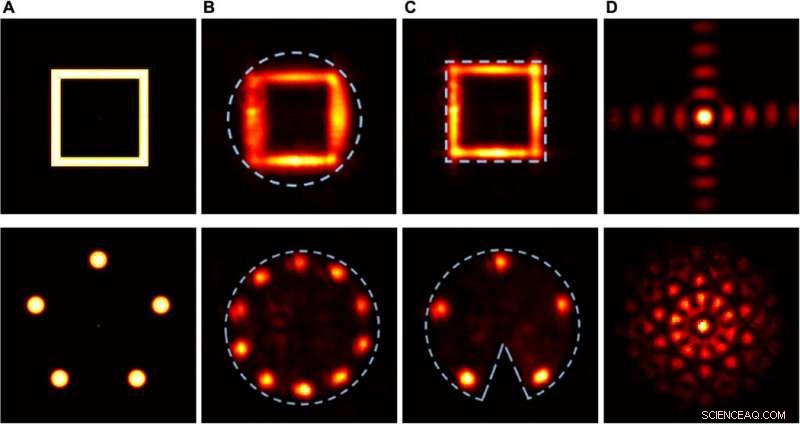 p Resultados experimentais demonstrando o efeito qualitativo de estanqueidade e assimetria de suportes compactos. Coluna (A) Distribuição da intensidade dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura quadrada como suporte compacto apertado (linha superior) e uma abertura circular com uma cunha como suporte compacto assimétrico (linha inferior). Coluna (D) Distribuições de intensidade de Fourier no SLM. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Resultados experimentais demonstrando o efeito qualitativo de estanqueidade e assimetria de suportes compactos. Coluna (A) Distribuição da intensidade dos objetos reais. Coluna (B) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura circular como suporte compacto. Coluna (C) Distribuição de intensidade detectada dos objetos reconstruídos, usando uma abertura quadrada como suporte compacto apertado (linha superior) e uma abertura circular com uma cunha como suporte compacto assimétrico (linha inferior). Coluna (D) Distribuições de intensidade de Fourier no SLM. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530
p Tradonsky et al mediram o efeito da complexidade do objeto na fidelidade da reconstrução e formaram distribuições de intensidade representativas para objetos com quatro, 16, e 30 pontos. Os resultados mostraram que objetos de maior complexidade (aqueles com mais pontos) apresentaram distribuição de intensidade de Fourier de maior complexidade, com detalhes intrincados que não poderiam ser resolvidos usando o sistema atual. Eles também observaram que as fidelidades de entrada e reconstrução diminuem com o aumento da complexidade do objeto, que eles creditaram ao ruído técnico flutuante da bomba de laser. Eles conduziram experimentos qualitativos para avaliar o efeito de aperto e simetria durante a reconstrução do objeto. Os resultados mostraram que um suporte compacto e apertado melhorou significativamente a qualidade do objeto reconstruído.
p A equipe investigou então os efeitos quantitativos do raio da abertura de suporte compacta na qualidade e fidelidade da reconstrução. Para objetos maiores, a intensidade representativa decaiu rapidamente durante a fidelidade da reconstrução, uma vez que o laser foi incapaz de suportar a forma do objeto. Com objetos menores do que a abertura de suporte compacta, Tradonsky et al observaram uma diminuição mais lenta da fidelidade. No total, eles observaram fidelidade de reconstrução reduzida quando a câmera calculou a média de várias realizações de um objeto dentro do sistema.
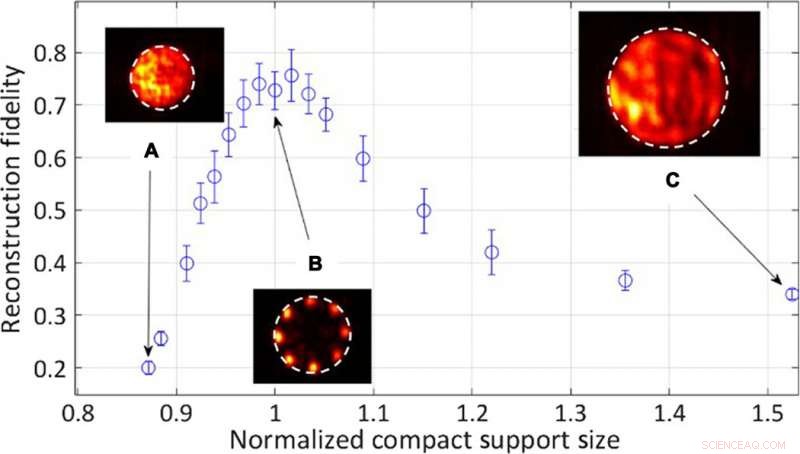 p Resultados quantitativos experimentais para a fidelidade da reconstrução em função do raio de suporte compacto da abertura normalizado pelo tamanho do objeto. Inserções:Distribuições típicas de intensidade de objetos reconstruídos. (A) O raio do suporte compacto é 87% do raio do objeto. (B) O raio do objeto é igual ao raio do suporte compacto. (C) O raio de suporte compacto é 152% do raio do objeto. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
p Resultados quantitativos experimentais para a fidelidade da reconstrução em função do raio de suporte compacto da abertura normalizado pelo tamanho do objeto. Inserções:Distribuições típicas de intensidade de objetos reconstruídos. (A) O raio do suporte compacto é 87% do raio do objeto. (B) O raio do objeto é igual ao raio do suporte compacto. (C) O raio de suporte compacto é 152% do raio do objeto. Crédito:Science Advances, doi:10.1126 / sciadv.aax4530.
p Geralmente, a resolução dos objetos reconstruídos foi relativamente baixa devido a aberrações de fase na cavidade do laser. A equipe propôs otimizar o sistema e reduzir as aberrações para melhorar a resolução. Os cientistas também analisaram o tempo gasto para oferecer uma solução de reconstrução usando o sistema e encontraram as durações ditadas pelo SLM (modulador de luz espacial) e a leitura da câmera em aproximadamente 20 ms. O tempo real de computação do lasing durou apenas menos de 100 nanossegundos. Quando Tradonsky et al otimizaram a configuração experimental usando um arranjo de laser de cavidade degenerada linear Q comutado com células pockel, eles reduziram o tempo total de computação do sistema para aproximadamente 100 nanossegundos. Comparativamente, o tempo de reconstrução com o algoritmo RAAR durou um segundo.
p Desta maneira. C. Tradonsky e colegas apresentaram um sistema óptico para recuperação rápida de fase usando um novo DDCL (laser digital de cavidade degenerada). O tempo de computação atingiu 100 nanossegundos; ordens de magnitudes mais rápidas do que o convencional, sistemas computacionais baseados em algoritmos. Com base nos resultados, várias modificações no sistema DDCL podem melhorar potencialmente seu desempenho, incluindo maior comprimento da cavidade do laser para aumentar o número de investigações paralelas independentes. A equipe de pesquisa irá explorar ainda mais o sistema para resolver uma variedade de problemas e resolver a qualidade da imagem após a propagação através de meios de espalhamento. p © 2019 Science X Network




