
Galáxia espiral M81. Crédito:NASA / JPL-Caltech / ESA / Harvard-Smithsonian CfA
O astrônomo do século 17 Johannes Kepler foi o primeiro a refletir sobre a estrutura dos flocos de neve. Por que eles são tão simétricos? Como um lado sabe quanto tempo o lado oposto cresceu? Kepler pensou que tudo se resumia ao que agora chamaríamos de "campo morfogênico" - que as coisas quer para ter a forma que eles têm. A ciência, desde então, descartou essa ideia. Mas a questão de por que os flocos de neve e estruturas semelhantes são tão simétricos não é totalmente compreendida.
A ciência moderna mostra o quão fundamental é a questão:olhe para todas as galáxias espirais lá fora. Eles podem ter meio milhão de anos-luz de diâmetro, mas eles ainda preservam sua simetria. Como? Em nosso novo estudo, publicado em Relatórios Científicos , apresentamos uma explicação.
Mostramos que a informação e a "entropia" - uma medida da desordem de um sistema - estão ligadas entre si ("info-entropia") de uma forma exatamente análoga aos campos elétricos e magnéticos ("eletromagnetismo"). As correntes elétricas produzem campos magnéticos, enquanto os campos magnéticos em mudança produzem correntes elétricas. A informação e a entropia influenciam-se mutuamente da mesma maneira.
Entropia é um conceito fundamental em física. Por exemplo, porque a entropia nunca pode diminuir (a desordem sempre aumenta), você pode transformar um ovo em ovos mexidos, mas não o contrário. Se você movimentar as informações, também deve aumentar a entropia - uma chamada telefônica tem um custo de entropia.
Mostramos que entropia e informação podem ser tratadas como um campo e que estão relacionadas à geometria. Pense nas duas fitas da dupla hélice do DNA enroladas uma em torno da outra. As ondas de luz têm a mesma estrutura, onde os dois fios são os campos elétrico e magnético. Mostramos matematicamente que a relação entre informação e entropia pode ser visualizada usando apenas a mesma geometria.

Floco de neve real. Crédito:Karen Schanely:https://www.clickinmoms.com/blog/take-macro-snowflakes-pictures/; domínio público
Queríamos ver se nossa teoria poderia prever coisas no mundo real, e decidiu tentar calcular quanta energia você precisaria para converter uma forma de DNA em outra. Afinal, o DNA é uma espiral e uma forma de informação.
Na verdade, isso foi feito em medições extraordinariamente precisas há cerca de 16 anos. Os pesquisadores puxaram uma molécula de DNA em linha reta (o DNA gosta de se enrolar), e torceu 4, 800 voltas segurando as pontas com pinças ópticas. O DNA mudou de uma forma para outra, como na foto acima. Os pesquisadores puderam então calcular a diferença de energia entre as duas formas.
Mas nossa teoria poderia calcular essa diferença de energia, também. Sabíamos a entropia de cada uma das duas versões desta molécula de DNA, e a energia é simplesmente o produto da entropia e da temperatura. Nosso resultado foi certeiro - a teoria parecia se sustentar.
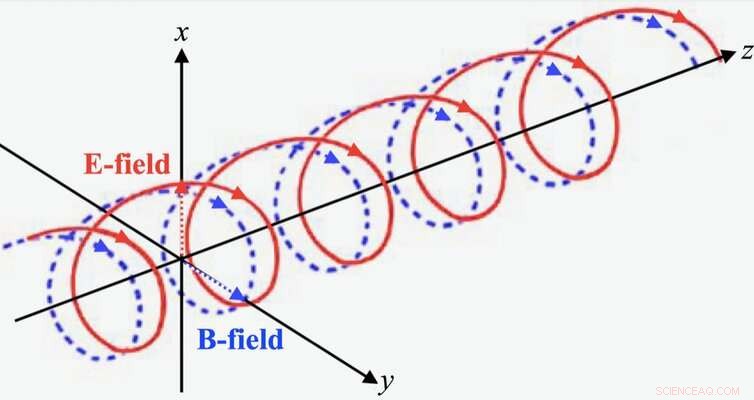
Onda de luz com campos elétricos (E) e magnéticos (B). Autor fornecido
De minúsculo a enorme
Galáxias espirais são espirais duplas, assim como o DNA é uma dupla hélice - matematicamente falando, elas têm geometrias semelhantes.
Nossa teoria mostra diretamente por que os dois braços das galáxias espirais são simétricos - é porque os campos de info-entropia dão origem a forças (como outros campos). As estrelas na galáxia são simplesmente coreografadas por uma força entrópica para se alinhar em um par de espirais para maximizar a entropia.
Mas queríamos alguns números reais, também. Portanto, decidimos tentar calcular a massa de nossa galáxia a partir de nossa teoria. Sabemos o quão pesada a Via Láctea parece ser pela velocidade com que as estrelas se movem perto da borda galáctica - tem cerca de 1,3 trilhão de massas solares.
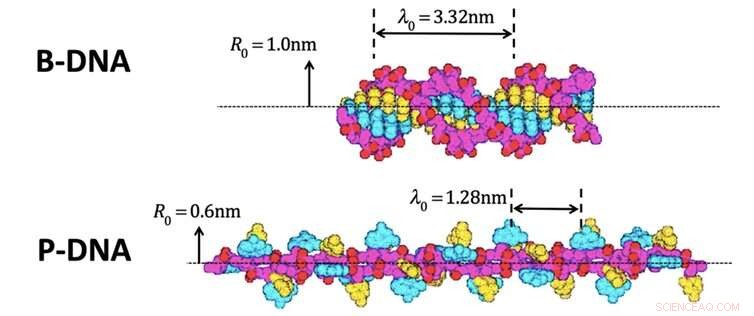
Duas formas de DNA. Crédito:Parker &Jeynes, Fig.1 de Scientific Reports 9 | 10779 (2019); Modificado da Fig. 5 de Allemand et al. Proc. Natl. Acad. Sci. EUA 95, 14152-14157 (1998), CC BY
Estranhamente, isso é na verdade muito mais do que a massa de todas as estrelas visíveis na galáxia. Para ser capaz de explicar essa discrepância e explicar por que as estrelas se movem muito mais rápido do que o esperado, astrônomos tiveram a ideia de "matéria escura" - massa invisível à espreita na galáxia, aumentando sua atração gravitacional sobre as estrelas.
Precisávamos saber a entropia da galáxia para nossos cálculos. Felizmente, o físico matemático Roger Penrose mostrou que essa entropia é dominada pela entropia de seu buraco negro supermassivo central.
Conhecemos a massa deste buraco negro (4,3 m de massas solares). E surpreendentemente, quando você conhece a massa de um buraco negro, há uma equação, descoberto pelo falecido físico Stephen Hawking, que calcula sua entropia. Hawking também descobriu como calcular a "temperatura" em sua superfície, ou "horizonte de eventos".
Se você pode atribuir uma "temperatura" ao horizonte de eventos do buraco negro - que não contém elementos para ter temperatura - por que não atribuir também uma temperatura a uma galáxia? Argumentamos em nosso artigo que isso é razoável (usando o que é conhecido como "princípio holográfico"). Então, usamos nossas equações de info-entropia para calcular a temperatura holográfica da galáxia.

Uma galáxia espiral com uma espiral logarítmica de dois braços sobreposta. Crédito:Parker &Jeynes, Fig.2 de Relatórios Científicos 9 | 10779 (2019), CC BY-SA
Então fica fácil. Sabemos que a energia galáctica é dada pelo produto de sua entropia e temperatura. E quando conhecemos a energia, podemos descobrir a massa graças à famosa equação de Einstein:E =mc 2 .
Desta vez, o resultado não foi exatamente correto, mas estava razoavelmente perto, dado nosso modelo altamente simplificado da galáxia. A geometria info-entrópica de uma galáxia não apenas explica como as forças entrópicas criam a forma simétrica lindamente e a mantêm, mas também é responsável por toda a massa que parece ser evidente nele.
Isso significa que, na verdade, não precisamos de matéria escura, afinal. De acordo com nosso modelo, a entropia galáctica dá origem a uma quantidade tão grande de energia adicional que modifica a dinâmica observada da galáxia - fazendo com que as estrelas na borda se movam mais rápido do que o esperado. Isso é exatamente o que a matéria escura deveria explicar. A energia não é diretamente observável como massa, mas sua presença é certamente apoiada pelas observações astronômicas - explicando por que as pesquisas de matéria escura até agora não encontraram nada.
No entanto, há muitas pesquisas apoiando a ideia da matéria escura. Nossa teoria sugere uma explicação alternativa das observações, e não precisa de nova física. Claro, um trabalho mais detalhado é necessário para verificar se a verdadeira complexidade das observações também pode ser modelada com sucesso.
Achamos que o "campo morfogênico" que Kepler estava procurando realmente existe, e é na verdade o efeito do entrelaçamento de informações e entropia. Depois de quatro longos séculos, parece que o Kepler finalmente foi justificado.
Este artigo foi republicado de The Conversation sob uma licença Creative Commons. Leia o artigo original. 