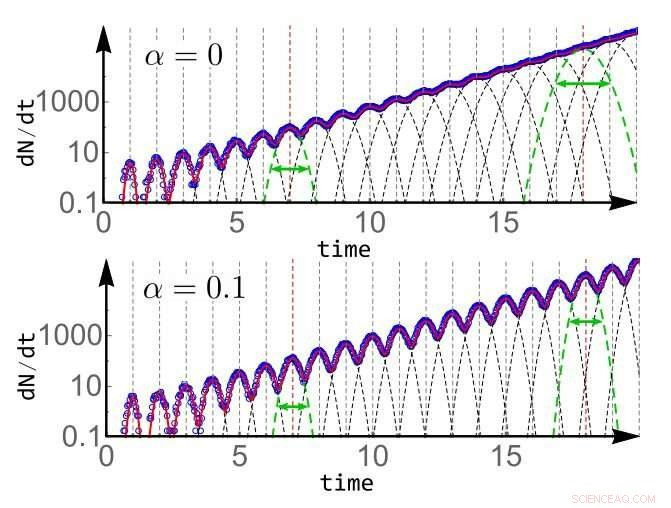
Gráfico de escala logarítmica do valor esperado da taxa de mudança do número de células em uma população começando com uma única célula, calculado analiticamente (curva sólida vermelha) e comparado com simulação (círculos azuis). A taxa de variação do número de células pode ser escrita como a soma das taxas de divisão (linhas tracejadas parabólicas) de todas as gerações. (Topo) Na ausência de controle de tamanho de célula, α =0, a distribuição dos tempos de divisão das gerações superiores fica mais ampla e começa a se sobrepor, amortecendo as oscilações na taxa de crescimento. (Embaixo) Na presença de até mesmo um controle de tamanho de célula pequeno, α =0,1, a distribuição de tempos de divisão sucessivos aproxima-se rapidamente de uma distribuição de estado estacionário com uma variância finita levando à persistência de oscilações no crescimento da população. A distribuição de tempo da 7ª e 18ª gerações é destacada em ambos os casos para comparação. Crédito:arxiv.org/pdf/1809.10217.pdf
Quando todos os casamentos familiares parecem coincidir uns com os outros, o fenômeno acontece por uma razão. Um indivíduo e seus primos-irmãos tendem a ser da mesma idade, então seus casamentos geralmente acontecem em um período de tempo semelhante. Mas casamentos para parentes, digamos primos de segundo e terceiro grau, tendem a ser mais espalhados. Isso ocorre porque o tempo entre uma geração para a próxima varia, o que significa que as famílias se espalham mais de geração em geração.
Um novo estudo do pós-doutorado Farshid Jafarpour da Universidade da Pensilvânia, do Departamento de Física e Astronomia, que trabalha no laboratório de Andrea Liu, revela que as variações nos tempos de geração não se acumulam ao longo de várias gerações em organismos unicelulares, como bactérias. Ele propõe uma nova teoria, publicado em Cartas de revisão física , que descreve como os fatores que regulam o tamanho das células individuais influenciam a taxa de crescimento de uma população inteira.
Ao contrário de animais e plantas, as bactérias aumentam o tamanho de sua população simplesmente crescendo em tamanho e depois se dividindo ao meio para formar duas novas células bacterianas. Ao estudar as bactérias quando se dividem regularmente, conhecida como fase de crescimento exponencial, Jafarpour foi capaz de desenvolver um modelo que descreve matematicamente esta fase fundamental do crescimento populacional. "Se você quiser estudar a física do crescimento bacteriano, você realmente deseja remover todas as outras partes que não fazem parte da fase de crescimento, " ele diz.
Jafarpour usou uma combinação de equações matemáticas, simulações de computador, e dados de experimentos de biologia que acompanharam o crescimento de células individuais de bactérias. Ele ficou surpreso ao descobrir que o modelo prevê que as bactérias oscilam entre explosões de crescimento mais lentas e mais rápidas, em "rajadas sincronizadas de divisões, "em vez de a população crescer a uma taxa constante. Essas oscilações no nível da população no crescimento agora fornecem um novo, forma matemática para os biólogos pensarem e estudarem a dinâmica populacional.
Anteriormente, os biólogos sabiam que o tempo de geração nas populações de bactérias estava diretamente relacionado ao tamanho das células individuais. Se uma bactéria cresce por muito tempo, por exemplo, suas células filhas são maiores, e eles devem se dividir mais cedo para compensar sua diferença de tamanho. Este processo, conhecido como regulação do tamanho da célula, também cancela parte da variabilidade no tempo de geração, que mantém os tempos de divisão sincronizados uns com os outros por um período de tempo muito mais longo do que o esperado anteriormente. É essa métrica individual de regulação do tamanho da célula que também parece estar causando as oscilações nas taxas de crescimento vistas no modelo de Jafarpour.
"A variabilidade nos tempos de geração tem duas fontes diferentes:a variabilidade no crescimento e a variabilidade na divisão, "Jafarpour explica." O resultado interessante é que a regulação do tamanho da célula está cancelando completamente a variabilidade na divisão, então a única coisa que resta é a variabilidade no crescimento das células individuais. E, porque é menor, as oscilações duram muito mais do que você esperaria. "
Este novo modelo agora pode ser usado por biólogos para obter informações sobre a variabilidade das taxas de crescimento individuais, que são difíceis de medir em laboratório, mas são extremamente importantes para estudar a evolução bacteriana. E embora este modelo precise de algumas modificações antes de poder ser usado para estudar outras espécies, Jafarpour acredita que ajudar os biólogos a obter um melhor entendimento da física que está por trás do crescimento populacional de bactérias é apenas uma das muitas maneiras pelas quais a física pode apoiar o trabalho realizado por biólogos.
"A biologia se tornou mais focada em descobrir a base molecular dos mecanismos desde 1950 com a descoberta da estrutura do DNA, mas agora estamos chegando a um nível em que temos que voltar e fazer mais estudos quantitativos. Os físicos têm uma longa tradição de trabalhar com sistemas do mundo real, saber como aplicar muitos dos métodos quantitativos desenvolvidos em matemática e também entender quais variáveis são relevantes e quais não são, "Jafarpour diz.