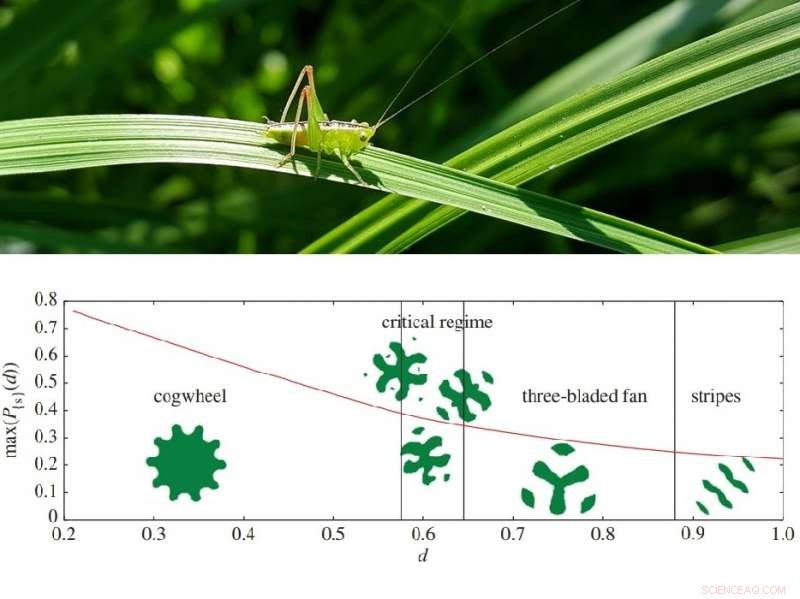
Algumas das formas ideais de gramado, que dependem da distância que o gafanhoto salta. Além do regime crítico, as melhores configurações são desconectadas. Crédito do diagrama:Goulko et al. The Royal Society. Crédito:Pixabay.
(Phys.org) —Como muitos quebra-cabeças matemáticos, o problema do gafanhoto é simples de declarar, mas difícil de resolver:um gafanhoto pousa em um ponto aleatório em um gramado da área 1, então pula uma vez, uma distância fixa, em uma direção aleatória. Qual deve ser o formato do gramado para maximizar a chance de o gafanhoto permanecer no gramado após o salto?
A primeira impressão pode ser a de que o gramado deve ter a forma de um círculo, pelo menos quando a distância que o gafanhoto salta é pequena. Contudo, Olga Goulko e Adrian Kent, os dois físicos que introduziram o problema do gafanhoto em um novo jornal, provaram matematicamente que um gramado em forma de disco não é ideal para qualquer distância.
Em vez de, eles descobriram por meio de simulações numéricas que a forma ideal do gramado assume uma variedade de formas complexas para diferentes distâncias de salto, como uma forma de roda dentada para distâncias menores que 1 / π 1/2 (o raio de um círculo de área 1, ou aproximadamente 0,56), enquanto para distâncias maiores, o gramado ideal consiste em peças desconectadas. Muitas vezes, Mas não sempre, essas formas ideais possuem algum tipo de simetria.
Motivado pela física
Além de ser um problema de geometria interessante, o problema do gafanhoto também está intimamente relacionado à pesquisa em física quântica e pode ter uma variedade de aplicações tecnológicas. Em particular, o problema do gafanhoto está conectado às desigualdades de Bell, que mostram isso, ao contrário dos modelos clássicos de física, a teoria quântica não obedece ao realismo local. Um excelente exemplo da violação do realismo local é visto no emaranhamento quântico, em que dois sistemas distantes e emaranhados exibem correlações que não podem ser explicadas por nenhum modelo que obedeça ao realismo local.
Esta conexão com as desigualdades de Bell é, na verdade, o que originalmente motivou Goulko e Kent a propor o problema do gafanhoto. Um problema aberto na física com relação às desigualdades de Bell é determinar os limites ótimos que são violados pela teoria quântica quando as correlações quânticas são medidas em uma esfera em ângulos entre 0 e 90 graus. Acontece que esse problema de determinar os limites ideais é equivalente ao problema de determinar a forma do gramado do problema do gafanhoto quando o gramado é esférico em vez de um terreno plano. Na versão esférica do problema do gafanhoto, a distância que o gafanhoto salta em terreno plano é substituída pelo ângulo em que ele salta através da esfera.
Em seu jornal, que é publicado em uma edição recente da Anais da Royal Society A , Goulko e Kent analisaram apenas a versão plana do problema do gafanhoto, embora eles esperem que não seja muito difícil aplicar as mesmas técnicas numéricas ao caso esférico. Então, ao considerar algumas restrições adicionais, pode ser possível resolver finalmente o problema dos limites ótimos das desigualdades de Bell.
"Pretendemos trabalhar nas versões esféricas do problema do gafanhoto relevantes para as desigualdades de Bell, e esperamos que nossos métodos funcionem lá, "Kent disse Phys.org .
Nova fronteira
Como explicam os físicos, uma das coisas surpreendentes sobre o problema do gafanhoto é que nada parecido jamais foi proposto antes. Embora a ideia básica seja direta o suficiente para que o problema pudesse ter sido colocado pelo antigo matemático grego Euclides, que lançou as bases da geometria moderna, os pesquisadores não têm conhecimento de nenhuma versão anterior do problema, tanto nos tempos antigos quanto nos modernos.
"É bom ser lembrado de que, mesmo em um campo tão antigo quanto a geometria, ainda é possível encontrar novas perguntas simples que têm respostas surpreendentes e abrem novas linhas de pesquisa, "Kent disse.
Como um novo problema, há um número infinito de direções de pesquisas futuras a serem seguidas. Por exemplo, os físicos sugerem que o gafanhoto dê vários saltos, ou exigir que o gafanhoto caminhe e permaneça no gramado em todos os pontos de seu caminho (variação que eles chamam de "problema da formiga"). Outras variações possíveis incluem generalizar para dimensões superiores, analisando as superfícies do gramado além de esferas e planos, considerando uma variação do problema com duas espécies diferentes de sementes de gramado que podem se sobrepor na mesma região (o que é particularmente relevante para as desigualdades de Bell), e colocar restrições adicionais às soluções possíveis.
Claro, tais questões não são realmente sobre gafanhotos e gramados, já que a estrutura subjacente oferece uma maneira de modelar várias situações do mundo real. Um exemplo apontado pelos pesquisadores são as reações em cadeia nuclear. Em uma reação em cadeia, uma partícula de alta energia impacta um núcleo atômico aleatório, fazendo com que sofra fissão, que produz outra partícula de alta energia que viaja uma certa distância para atingir outro núcleo aleatório, e o processo se repete. Ao modelar esta situação com o problema do gafanhoto, a área ótima do gramado corresponde à taxa de reação inicial máxima, o que maximiza o número de núcleos que participam da reação em cadeia.
Outra aplicação potencial do problema do gafanhoto está na modelagem de protocolos de comunicação quântica, que os pesquisadores explicam pode ser pensado como um modelo de gafanhoto no qual uma parte deve escolher qual algoritmo (formato do gramado) usar para se comunicar com uma segunda parte.
E finalmente, os pesquisadores sugerem que pode ser interessante observar as próprias origens das formas do gramado, como alguns dos padrões do gramado se assemelham a padrões que surgem repetidamente na natureza, como nas flores, conchas do mar, e listras de animais. De acordo com a teoria da morfogênese proposta por Alan Turing, esses padrões podem surgir como soluções ideais por razões químicas, o que pode ajudar a explicar as formas diversas e complexas dos gramados que aparecem no problema do gafanhoto.
© 2017 Phys.org