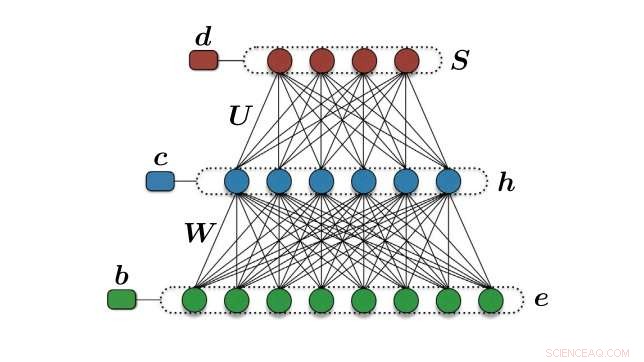
A arquitetura do decodificador neural. Crédito:Torlai et al. © 2017 American Physical Society
(Phys.org) —Os físicos aplicaram a capacidade dos algoritmos de aprendizado de máquina para aprender com a experiência a um dos maiores desafios que a computação quântica enfrenta atualmente:correção de erros quânticos, que é usado para projetar protocolos de computação quântica tolerantes a ruído. Em um novo estudo, eles demonstraram que um tipo de rede neural chamada máquina de Boltzmann pode ser treinada para modelar os erros em um protocolo de computação quântica e, em seguida, desenvolver e implementar o melhor método para corrigir os erros.
Os físicos, Giacomo Torlai e Roger G. Melko da Universidade de Waterloo e do Perimeter Institute for Theoretical Physics, publicaram um artigo sobre o novo algoritmo de aprendizado de máquina em uma edição recente da Cartas de revisão física .
"A ideia por trás da decodificação neural é contornar o processo de construção de um algoritmo de decodificação para uma realização de código específico (dadas algumas aproximações sobre o ruído), e deixe uma rede neural aprender como realizar a recuperação diretamente de dados brutos, obtido por medições simples no código, "Torlai disse Phys.org . "Com os avanços recentes nas tecnologias quânticas e uma onda de dispositivos quânticos se tornando disponíveis em curto prazo, decodificadores neurais serão capazes de acomodar as diferentes arquiteturas, bem como diferentes fontes de ruído. "
Como explicam os pesquisadores, uma máquina de Boltzmann é um dos tipos mais simples de redes neurais artificiais estocásticas, e pode ser usado para analisar uma ampla variedade de dados. As redes neurais normalmente extraem recursos e padrões de dados brutos, que, neste caso, é um conjunto de dados contendo os possíveis erros que podem afetar os estados quânticos.
Uma vez que o novo algoritmo, que os físicos chamam de decodificador neural, é treinado com esses dados, é capaz de construir um modelo preciso da distribuição de probabilidade dos erros. Com esta informação, o decodificador neural pode gerar as cadeias de erro apropriadas que podem então ser usadas para recuperar os estados quânticos corretos.
Os pesquisadores testaram o decodificador neural em códigos topológicos quânticos que são comumente usados em computação quântica, e demonstrou que o algoritmo é relativamente simples de implementar. Outra vantagem do novo algoritmo é que ele não depende da geometria específica, estrutura, ou dimensão dos dados, o que permite que seja generalizado para uma ampla variedade de problemas.
No futuro, os físicos planejam explorar diferentes maneiras de melhorar o desempenho do algoritmo, como empilhar várias máquinas Boltzmann umas sobre as outras para construir uma rede com uma estrutura mais profunda. Os pesquisadores também planejam aplicar o decodificador neural a mais complexos, códigos realistas.
"Até aqui, decodificadores neurais foram testados em códigos simples normalmente usados para benchmarks, "Torlai disse." Uma primeira direção seria realizar a correção de erros em códigos para os quais um decodificador eficiente ainda não foi encontrado, por exemplo, códigos de verificação de paridade de baixa densidade. No longo prazo, acredito que a decodificação neural desempenhará um papel importante ao lidar com sistemas quânticos maiores (centenas de qubits). A capacidade de compactar objetos de alta dimensão em representações de baixa dimensão, que deriva do sucesso do aprendizado de máquina, permitirá capturar fielmente a distribuição complexa relacionando os erros que surgem no sistema com os resultados das medições. "
© 2017 Phys.org