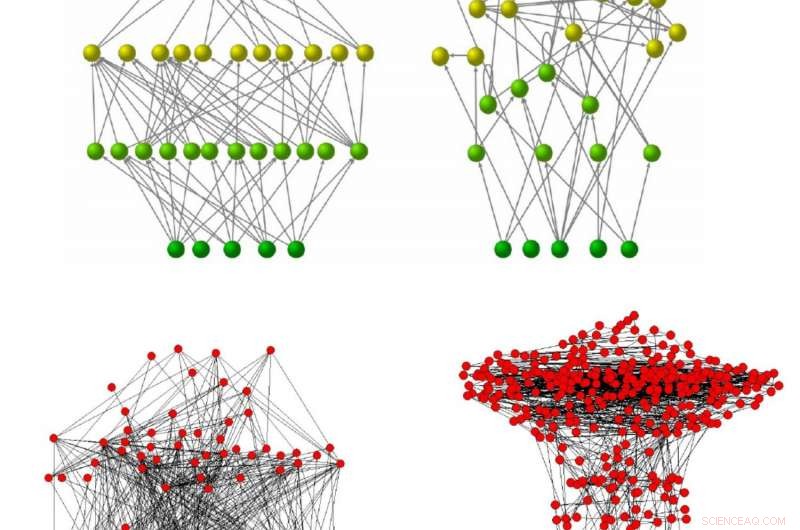
Quatro redes dirigidas, plotado de forma que a altura de cada nó no eixo vertical seja proporcional em cada caso ao seu nível trófico. Os dois principais são redes sintéticas, gerado em um computador com o "modelo de caça preferencial", que permite ao usuário ajustar a coerência trófica (medida com o parâmetro de incoerência, q). Assim, ambos têm o mesmo número de nós e arestas, mas o da esquerda é perfeitamente coerente (q =0), enquanto o da direita é mais incoerente (q =0,7). Os dois últimos são derivados empiricamente:o da esquerda é a teia alimentar do Estuário de Ythan, o que é significativamente coerente (tem q =0,42, que é cerca de 15% de seu q esperado) e pertence ao regime "sem loop"; o da direita é uma representação da rede metabólica de Chlamydia pneumoniae, o que é significativamente incoerente (q =8,98, ou cerca de 162% da expectativa aleatória) e fica no regime "loopful". As duas redes principais são reproduzidas do Apêndice SI de Johnson et al, “A coerência trófica determina a estabilidade da teia alimentar” ( PNAS , 2014), enquanto os dois últimos são do Apêndice SI de Johnson &Jones, “Looplessness nas redes está ligado à coerência trófica” ( PNAS , 2017). Cortesia:Dr. Samuel Johnson.
(Phys.org) —Complexidade - definida como tendo propriedades emergentes ou características que não são uma função de, e são, portanto, difíceis ou inerentemente impossíveis de prever, os componentes discretos que compõem o sistema - é uma característica de sistemas complexos em uma ampla gama de escalas (como genes, neurônios e outras células, cérebros, computadores, língua, e ecossistemas naturais e sociopolíticos) que compreendem elementos interconectados capazes de automodificação por meio de ciclos de feedback. Ao mesmo tempo, existem redes (biológicas e outras) que têm muito menos desses loops do que o esperado - mas, embora essas redes de loop de feedback baixo sejam conhecidas por apresentarem alta estabilidade, o mecanismo de supressão de feedback (que confere essa estabilidade) permaneceu não identificado. Recentemente, Contudo, cientistas da University of Warwick e Imperial College London mostraram que o nível de feedback em sistemas complexos é uma função de coerência trófica - uma propriedade que revela a distribuição de nós em níveis de rede de alto e baixo feedback.
O Dr. Samuel Johnson discutiu o artigo que ele e o Dr. Nick S. Jones publicaram em Proceedings of the National Academy of Sciences . "Demonstrar que a coerência trófica é uma propriedade encontrada em uma ampla gama e escala de ecossistemas e redes foi realmente mais fácil do que esperávamos, "Johnson diz Phys.org . "Nós identificamos anteriormente a coerência trófica como uma propriedade importante das teias alimentares 1 , em que nosso principal resultado foi o papel da coerência trófica na estabilidade do ecossistema. "(Teias alimentares são redes de ecossistemas de níveis tróficos de espécies - isto é, o que uma espécie come, e o que é comido - e de fato, a palavra trófico deriva do grego τροφή (pronunciado troféuē ), que se refere a comida ou nutrição.) "Os ecologistas há muito caracterizam as espécies em cadeias alimentares por seus níveis tróficos, portanto, a ideia de medir o quão bem definidos esses níveis eram parecia muito natural. "
Contudo, ele aponta que, embora os pesquisadores tenham, nos últimos 15 anos ou mais, definiu e estudou muitas quantidades associadas a redes complexas, parece que o papel dos níveis tróficos em outras redes além das cadeias alimentares não foi estudado. "Tudo o que tivemos que fazer foi obter os dados que outros pesquisadores disponibilizaram para vários tipos diferentes de redes, e medir os níveis tróficos e a coerência associados a eles, ele explica. "Então, quando começamos a desenvolver uma estrutura matemática que pudesse relacionar a coerência trófica com outras quantidades de rede, uma das primeiras etapas foi derivar equações para os valores esperados de coerência trófica e níveis tróficos médios em gráficos aleatórios - isto é, os valores que esperaríamos que uma rede tivesse se as arestas tivessem sido colocadas aleatoriamente entre os nós. Isso, por sua vez, nos permitiu investigar uma determinada rede empírica e concluir, por exemplo, se era mais ou menos coerente do que se fosse aleatório. "
Em relação à derivação de expressões matemáticas analíticas que mostram que a ausência de loop é uma consequência provável da coerência trófica, Johnson reconta, os cientistas puderam ver intuitivamente - ou desenhando imagens de redes com maior e menor coerência - que essa propriedade estava relacionada ao número provável de ciclos (ou loops) em redes direcionadas (ou seja, aqueles em que os links, ou bordas, tem uma direção). Para estudar esta relação matematicamente, ele adiciona, eles empregaram o método da física estatística de conjuntos - coleções virtuais de um grande a infinito número de sistemas idênticos cujo comportamento é inferido do comportamento agregado do conjunto - que tem sido usado para estudar gráficos aleatórios.
Os cientistas dão crédito a um momento que se provou fundamental para sua investigação. "Nosso insight crucial foi que, dada sua coerência trófica, poderíamos associar o número esperado de ciclos em uma rede, com a probabilidade de que um tipo particular de caminhante aleatório em uma linha voltaria ao seu ponto de partida. "Caminhantes aleatórios - objetos imaginários cujo movimento é determinado uma seleção aleatória entre duas ou mais escolhas em cada incremento, ou saltar . "Caminhantes aleatórios provaram conceitos úteis em uma ampla gama de contextos, "Johnson observa, "da explicação de Albert Einstein do movimento browniano que provou a existência de moléculas, ao algoritmo PageRank de Sergei Brin e Larry Page que deu origem ao Google. No nosso caso, definimos caminhantes aleatórios cujos saltos foram retirados de uma distribuição centrada em um e com desvio padrão igual à incoerência trófica da rede. prevalência de loops na rede associada.
Com este método, Johnson conta Phys.org , eles foram capazes de obter expectativas e distribuições de probabilidade para várias quantidades de interesse em função da coerência trófica, que eles chamaram de conjunto de coerência . Além disso, eles descobriram que uma vez que a coerência trófica foi levada em consideração, o número de ciclos e magnitudes relacionadas medidos em todas as redes empíricas que eles estudaram estavam muito próximos de suas expectativas teóricas. "A partir disso, fomos capazes de concluir que a coerência trófica e propriedades como loopless" (que eles definem vagamente como tendo poucos ou nenhum ciclo) "estavam intimamente relacionadas.
"Poderia, claro, Seja o caso, "Johnson reconhece, "que certas classes de redes reais são coerentes como consequência de algum processo que suprimiu ciclos. Por exemplo, "ele ilustra, "se os ecossistemas com muitos ciclos tendem a se tornar instáveis e entrar em colapso, então, talvez apenas os sem loop sobreviveram, e a coerência trófica veio daí. Contudo, quando geramos redes em um computador para não ter ciclos, descobrimos que isso não induz coerência trófica, enquanto aqueles gerados para serem suficientemente coerentes são sem loop. "Os pesquisadores concluíram, portanto, que os mecanismos de indução de coerência são mais provavelmente responsáveis pela ausência de loop na natureza.
Além dos exemplos de ausência de alças resultantes da coerência trófica mencionados em seu artigo, Johnson discutiu várias classes de redes nas quais os níveis tróficos estão provavelmente relacionados a algum tipo de função de nó, como parece ocorrer com a função sintática em grafos de adjacência de palavras. "Esperamos que, se pudéssemos obter dados sobre esses sistemas, podemos descobrir que sua coerência trófica ou incoerência desempenha um papel em seu comportamento, por meio de seus efeitos sobre loopless ou loopfulness, conforme o caso. Mais amplamente, acreditamos que classificar os nós em tais redes por nível trófico pode ser útil, como é o caso dos ecossistemas. "Por exemplo, ele ilustra, as relações de poder entre pessoas em vários tipos de organizações podem seguir esse padrão. "Imagine um exército, uma corporação, ou toda uma sociedade, em que cada pessoa é um nó e uma borda direcionada ( também conhecido como seta) aponta de cada indivíduo para aqueles a quem eles se reportam, ou devo algum tipo de obediência. O nível trófico de uma pessoa daria uma indicação de sua posição hierárquica, e talvez a coerência trófica de todo o sistema possa estar relacionada à velocidade de transmissão da informação ou sua robustez a revoltas. Estamos pensando nisso no momento. "
Os cientistas também esperam estudar o significado dos níveis tróficos nas redes neurais. "Incluímos apenas um exemplo em nosso artigo - o muito estudado cérebro do C. elegans worm - mas estamos interessados em efeitos nas habilidades computacionais, em que os loops de feedback podem ser muito importantes. É curioso que as redes neurais usadas para aprendizado profundo sejam perfeitamente coerentes - então, o que um pouco de incoerência pode fazer? "
Embora não seja discutido neste artigo, Johnson e Phys.org discutiu a questão de saber se o número de loops feedforward de um sistema é afetado pela coerência trófica. "É muito interessante você perguntar isso! Como parte de seu trabalho de doutorado, Janis Klaise está examinando essa questão - e temos um artigo enviado mostrando que esse é realmente o caso. Já se sabe há algum tempo que se estudarmos os perfis de motivos das redes empíricas - isto é, a prevalência de cada uma das maneiras possíveis nas quais trigêmeos de nós podem ser conectados - existem várias famílias amplas de redes com perfis semelhantes. "Existem dois grupos principais de teias alimentares, ele ilustra, diferindo principalmente em se o loop feedforward está sub ou super-representado, correspondendo assim a teias alimentares mais ou menos troficamente coerentes, respectivamente.
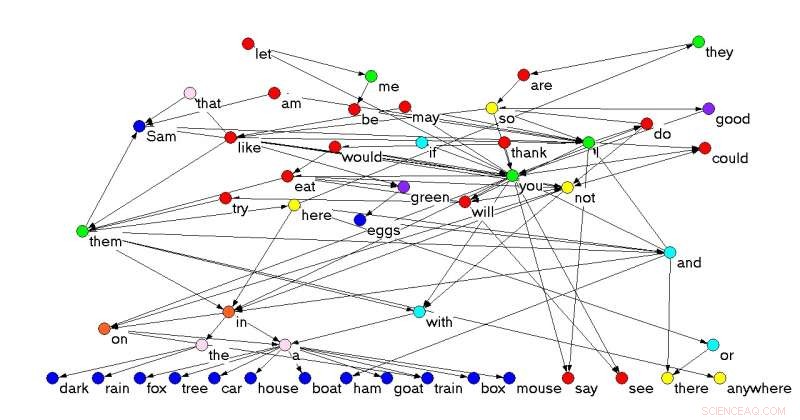
Rede de palavras concatenadas de Ovos verdes e presunto , pelo Dr. Seuss [3]. A altura de cada palavra é proporcional ao seu nível trófico. As cores indicam a função sintática; do nível trófico médio mais baixo ao mais alto:substantivos (azul), preposições e conjunções (ciano), determinantes (rosa), advérbios (amarelo), pronomes (verde), verbos (vermelho), e adjetivos (roxo). Quando uma palavra tem mais de uma função, o mais comum no texto é usado. Crédito:Johnson S, Jones NS (2017) Looplessness em redes está ligado à coerência trófica. Proc Natl Acad Sci USA 114 (22):5618-5623.
O impacto deste ponto, Johnson continua, baseia-se no fato de que os loops de feedforward muitas vezes podem estar relacionados a alguma forma de controle de feedforward (como usado, ele observa, por engenheiros que trabalham na direção assistida de automóveis). "Portanto, loops feedforward em certas redes biológicas - redes reguladoras de genes, em particular, mas também outros, como redes neurais - são considerados para desempenhar um papel importante em como esses sistemas funcionam. Em teias alimentares, loops feedforward estão associados a espécies onívoras, que muitas vezes tem sido relatado como tendo um efeito na estabilidade do ecossistema - embora alguns digam que o efeito é positivo e outros negativo! "
Os pesquisadores também estão investigando se neguentropia - o oposto da entropia, e em que um físico, processos termodinâmicos ou biológicos criam ordem - são afetados pela coerência trófica. "O conceito moderno de entropia, "Johnson aponta, "vem da física estatística e é uma propriedade de conjuntos, conforme descrito acima - isto é, a entropia de um conjunto é simplesmente uma função do número de elementos que ele contém. "Além disso, ele adiciona, A entropia de conjunto de grafos provou ser uma ferramenta poderosa para a compreensão de várias propriedades de rede. Atualmente, estamos estudando a entropia do conjunto de coerência que definimos para este trabalho. "Em geral, maior coerência trófica estaria associada a estados de entropia mais baixos, o que significa que, se as redes são mais coerentes do que a expectativa aleatória, deve realmente haver algum tipo de processo negentrópico em ação. "Johnson observa que o impacto, neste caso, relativo à coerência trófica seria encontrado na quantificação da extensão em que diferentes redes empíricas têm foram retirados de seu estado de entropia máxima. "Esta pode ser a melhor maneira de descobrir quando há mecanismos indutores de coerência em funcionamento, quanta energia deve estar envolvida, e, em última análise, identificar a natureza de tais processos. "
Phys.org também perguntou a Johnson se há limites de escala para a coerência trófica - por exemplo, é a coerência trófica aplicável a sistemas ou estruturas em nanoescala, ou para a mecânica quântica (na qual os autovalores são altamente relevantes)? "Esta é uma pergunta interessante, "ele respondeu." Não pensamos muito sobre isso ainda - mas não há nenhuma razão, em princípio, para que a coerência trófica não seja relevante em outros ambientes além dos que consideramos, e em outras escalas. Embora estejamos pensando sobre a coerência trófica como uma propriedade das redes, poderia ser facilmente considerado como uma propriedade de matrizes, que têm muitas interpretações e aplicações diferentes na ciência. O conceito de coerência trófica poderia ser estendido ao complexo, Matrizes hermitianas que descrevem operadores quânticos, por exemplo? "(Uma matriz Hermitiana é uma matriz quadrada auto-adjunta equivalente à sua própria transposta conjugada.)" Em caso afirmativo, o que significaria o efeito da coerência em eigenspectra para observáveis físicos? Esperamos que essas e outras questões em aberto atraiam a atenção de pesquisadores nas áreas relevantes, que pode ser capaz de levar o trabalho mais longe. "
Johnson também observou que, embora certos sistemas naturais não sejam surpreendentes, dada sua coerência trófica, Isso não é sempre o caso. "A maioria das coisas que medimos em nosso conjunto de redes empíricas estava realmente perto do que preveríamos, dada sua coerência trófica. As exceções foram algumas teias alimentares que, curiosamente, não tem ciclos, apesar de estar no regime de loopful - mas isso não implica, por qualquer meio, que tudo é determinado pela coerência trófica de uma rede, visto que existem muitas outras quantidades que ainda não consideramos. O que foi um tanto surpreendente, Contudo, foi que, embora as redes de regulação gênica pareçam altamente coerentes, eles estão todos muito próximos do que seria sua expectativa aleatória, o que se deve à tendência de terem muitos nós basais. "Johnson explica que essas redes - que ele diz serem a base de todos os processos que as células são capazes de realizar, e determinar os vários tipos de células em que eles podem se transformar - devem ter sido ajustados pela evolução de inúmeras maneiras. "Parece, portanto, surpreendente que sua coerência trófica mostra pouco desvio de nossa expectativa aleatória. Por outro lado, as redes metabólicas são todas altamente incoerentes, em comparação com a expectativa aleatória, mas ainda não temos ideia do porquê disso. "
Outros mecanismos indutores de coerência ou incoerência presumivelmente alterariam uma rede de tal forma que a probabilidade de uma borda ocorrer entre dois nós depende de seus níveis tróficos, ele continua, apontando que isso pode acontecer porque os níveis tróficos refletem alguma outra característica do nó, sua função intranetwork, ou sua posição em uma ou mais dimensões. "Por exemplo, no caso de teias alimentares, "ele ilustra, "existem várias características biológicas das espécies que estão relacionadas aos níveis tróficos, então é natural que se um determinado predador se especializou em consumir a espécie A, é mais provável que caia também em B se A e B estiverem em níveis semelhantes. Contudo, em alguns ecossistemas, as espécies também podem ocupar diferentes posições no espaço - por exemplo, eles podem existir em diferentes profundidades em um lago - o que também pode afetar a coerência. Além disso, em uma rede social, as pessoas podem interagir com outras de acordo com seu trabalho, ou seu status - mas neurônios, genes, ou palavras em um texto são conectadas a outras, que têm funções funcionais específicas. Embora esperássemos encontrar mecanismos que levassem à formação de arestas preferencialmente entre nós de acordo com esses tipos de recursos, funções, ou dimensões, provavelmente existem outras maneiras que ainda não pensamos. "
Outra questão é como conceitos como coerência trófica podem ser entendidos quando uma distinção entre interações excitatórias e inibitórias é feita. "Existem pelo menos duas maneiras pelas quais pode ser útil definir os níveis tróficos, e, portanto, coerência, nesse caso. Um seria simplesmente atribuir um valor negativo às interações inibitórias, mas mantenha outras definições basicamente iguais, de modo que os níveis tróficos podem ser positivos ou negativos, "Johnson diz Phys.org . "Outra é separar os efeitos das interações excitatórias e inibitórias como se estivessem em redes diferentes, de modo que cada nó teria dois níveis tróficos diferentes, e haveria uma coerência excitatória e outra inibitória. Isso se encaixa com o trabalho que está sendo feito atualmente nas chamadas redes multiplex. No fim, teríamos que ver qual definição se mostra mais útil para entender as redes do mundo real. "
Seguindo em frente, Johnson diz, ele e seus colegas estão investigando caminhos que decorrem da pesquisa em discussão, como estender os conceitos de níveis tróficos e coerência a uma classe mais ampla de redes - por exemplo, aqueles com bordas ponderadas ou muitas camadas. "Esperamos, então, usá-los em conjunto com outras medidas de rede bem estabelecidas para identificar grupos funcionais de nós em sistemas específicos, como redes reguladoras de genes ou ecossistemas. Outro de nossos interesses é a integração desses resultados dentro de um arcabouço matemático mais geral, relacionando estrutura e dinâmica em sistemas complexos. Finalmente, "ele conclui, "há questões na ecologia que este trabalho pode iluminar, incluindo a melhor forma de modelar teias alimentares, e se existem propriedades de rede de ecossistemas que podem nos alertar para o risco de um ponto de inflexão, como uma cascata de extinções. "
Johnson acrescenta que ele e Jones estão trabalhando em vários outros tópicos, bem como em redes. "Por exemplo, Tenho várias colaborações em andamento com pessoas em Warwick e Granada, investigando a relação entre conflito humano e geografia, ou como certas descobertas da neurociência podem ser compreendidas e modeladas matematicamente. "
Em relação a outras áreas de pesquisa que podem se beneficiar de seu estudo, Johnson diz que o mais imediato seria redes complexas e teoria dos grafos, onde nossos resultados devem ser do interesse de pessoas que estudam conjuntos de gráficos, as relações entre as diferentes quantidades topológicas, ou a estabilidade do complexo, sistemas dinâmicos. "Como acima mencionado, existem alguns resultados que são particularmente relevantes para ecologistas, especialmente aqueles envolvidos na modelagem de ecossistemas. Esperamos que algumas dessas ideias sejam captadas por pesquisadores em outras áreas onde os sistemas podem ser considerados como redes de maneira proveitosa - eu mencionei a genética, mas existem vários outros, como a neurociência, sociologia, ou economia - e desenvolvido ainda mais. "
© 2017 Phys.org