
Crédito:Universidade de Connecticut
Quem disse que as regras foram feitas para serem quebradas não era físico. Quando algo não age da maneira que você acha que deveria, ou as regras estão erradas, ou há uma nova física a ser descoberta. Que é exatamente o que Connor Occhialini da UConn, um estudante sênior homenageia estudante com especialização em física e matemática, encontrado quando ele começou a pesquisar o fluoreto de escândio.
O fluoreto de escândio é um cristal transparente com forma cúbica, um subproduto da mineração. Não é usado comercialmente e não seria particularmente interessante para ninguém, exceto por uma coisa estranha:ele encolhe à medida que aquece.
A maioria dos materiais incha à medida que aquece. Materiais realmente simples como o gás hidrogênio incham porque o calor faz seus átomos girarem mais rápido, esbarrando mais uns nos outros, portanto, o mesmo número de átomos de hidrogênio precisa de mais espaço. Materiais mais complicados também incham, É por isso que sua porta da frente de madeira tende a travar no verão. Mas sólidos como a madeira não podem inchar tanto quanto um gás porque seus átomos estão fortemente ligados entre si em longos, moléculas interligadas, então eles apenas se mexem, inchando a porta um pouco.
O fluoreto de escândio deve estar fazendo outra coisa, raciocinou Occhialini. Seu conselheiro para seu projeto de física de honra, Jason Hancock, tem trabalhado com fluoreto de escândio, e pediu a Occhialini para estudar um modelo da dinâmica do cristal. O fluoreto de escândio tem uma estrutura bastante simples:é um cristal sólido, com cada átomo de escândio rodeado por seis flúores para fazer pilhas de octaedros (diamantes de oito lados). Os pesquisadores esperavam que a estrutura simples fosse fácil de entender. Compreendendo a estranha 'expansão térmica negativa do fluoreto de escândio, 'como os físicos chamam o encolhimento relacionado ao calor, pode gerar uma visão mais geral sobre outros, materiais mais complexos que fazem a mesma coisa.

Figura 1. Ajuda, Estou encolhendo! Os diamantes negros representam moléculas de fluoreto de escândio. Enquanto eles aquecem, eles giram, e os contratos de cristal. Observe como as moléculas perto do centro de massa (ponto central) se movem menos do que as moléculas mais próximas da borda do cristal. Crédito:Universidade de Connecticut
O primeiro passo de Occhialini foi simplificar o problema. Então, em vez de um cristal tridimensional, ele decidiu pensar nisso como uma folha bidimensional.
Cada diamante preto representa uma molécula de fluoreto de escândio. Os átomos de escândio (pontos azuis) estão no centro de cada diamante, e um átomo de flúor está em cada canto.
A maior parte do tempo, ligações entre átomos são flexíveis. Portanto, em um sólido cristalino normal - fluoreto de cálcio, por exemplo - os átomos de flúor e cálcio seriam todos capazes de se mexer independentemente quando o material aquecesse. Enquanto eles se mexiam, eles ocupariam um pouco mais de espaço, e o sólido aumentaria. Comportamento sólido normal.
Mas Occhialini se perguntou se talvez não fosse isso o que estava acontecendo com o fluoreto de escândio. Talvez neste modelo, ele deveria presumir que as ligações entre cada flúor e seu escândio eram rígidas? Tão rígidas, as ligações de flúor-escândio não se movem, então os diamantes são como blocos sólidos. Os únicos lugares em que a estrutura seria capaz de flexionar quando aquecesse seriam nos átomos de flúor, que agiriam como pequenas articulações. Conforme o cristal esquentava, os pequenos blocos de fluoreto de escândio se inclinariam em torno dos flúores nos cantos. Isso é o que você vê acontecendo na foto. Você notará que quando os diamantes se inclinam, toda a estrutura fica menor. Na verdade, ele fica mais tenso. O contorno azul mostra a estrutura mais fria, estado perfeitamente ordenado, sem movimento molecular. Quando os diamantes se inclinam, eles ocupam um volume total menor do que o delineado pelo contorno azul. Esta é a expansão térmica negativa.
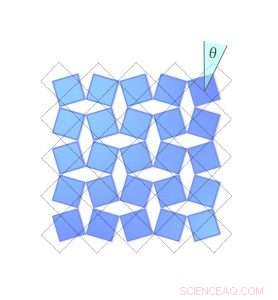
Figura 2. O quanto um cristal de fluoreto de escândio encolhe depende de quão longe as moléculas giram. Aqui, o diamante azul no canto superior direito está girando no sentido horário, varrendo um ângulo theta. As linhas pontilhadas mostram sua posição quando o ângulo era zero. Crédito:Universidade de Connecticut
Occhialini descobriu que você pode descrever esse encolhimento matematicamente, usando apenas o ângulo de inclinação das moléculas. Ele chamou o ângulo de Θ (theta). Quando o fluoreto de escândio bloqueia a inclinação em um ângulo Θ, a distância entre o centro de cada bloco diminui por um fator de cosseno Θ, e o volume total do cristal diminui.
Para calcular essa redução (ou, em um material normal, expansão) em detalhes, Occhialini acrescentou um terceiro termo à equação clássica que descreve a energia de um cristal vibrante. Os primeiros dois termos na equação padrão descrevem a energia potencial que um cristal tem da curvatura em cada junção molecular, mais a energia cinética de rotação de cada molécula. A equação de Occhialini também descreve a energia cinética translacional das moléculas - não apenas da rotação, mas também se aproximando e se afastando de suas posições originais à medida que giram. Quanto mais longe eles estão do centro de massa do cristal, quanto mais eles se movem. Olhe novamente para a Figura 1 e observe o ponto no meio; esse é o centro de massa. Os diamantes no meio mal se movem em relação a ele, enquanto os diamantes nas bordas se movem muito. Agora imagine quanta diferença haveria se o cristal tivesse milhões de moléculas em vez de apenas 25. E agora você entende como esse terceiro termo poderia ser importante para a energia do cristal.
Agora, moléculas sendo moléculas, eles não apenas encolhem e permanecem lá. Eles estão se movendo constantemente, e quanto mais aquecidos ficam, quanto mais eles se movem. Parte da visão de Occhialini é que, na média, a estrutura molecular fica mais curvada quanto mais quente fica. Assim, as moléculas se inclinam mais e passam mais tempo em valores maiores de Θ, mais perto de 45 graus. Depois que Occhialini refletiu por um tempo junto com Hancock e os alunos de doutorado em física Sahan Handunkanda e Erin Curry, eles perceberam que havia uma forma geométrica com a mesma descrição matemática. É o pêndulo em espiral de Arquimedes.
Cada volta da espiral está exatamente à mesma distância da última. Esse espaçamento - a distância entre as voltas - é controlado por Θ. Imagine uma linha que se estende do centro da esfera até um ponto na espiral. O ângulo entre essa linha e o pólo da esfera é Θ. Você vê a bolinha viajando ao longo da espiral? É o fim da linha imaginária. À medida que Θ fica maior, a bola se move em direção ao equador. Imagine que a bola representa o estado instantâneo do cristal de fluoreto de escândio - os físicos calcularam a média estatística do que cada molécula do cristal está fazendo. Você notará que a bola passa mais tempo perto do equador da esfera espiral, isso é, tende a sair onde Θ é grande. Se a temperatura do cristal cair e as moléculas se mexerem menos, Θ fica menor, quanto mais tempo a bola passa perto do pólo da esfera e menos o cristal encolhe.
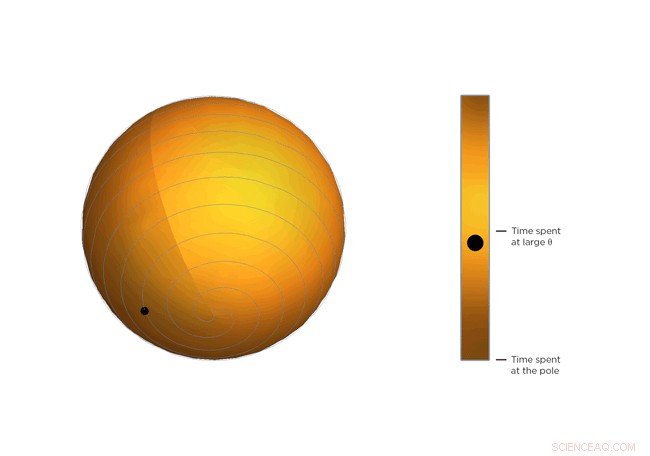
Figura 3. Torça e encolha. A equação que descreve a rotação das moléculas de fluoreto de escândio é a mesma que a equação que descreve o movimento de uma bola em um pêndulo espiral de Arquimedes. Observe como ele passa mais tempo em ângulos maiores. Crédito:Universidade de Connecticut
Portanto, não só pode um fenômeno realmente estranho de um cristal que encolhe à medida que aquece ser explicado apenas assumindo que as moléculas são rígidas, mas pode ser ilustrado com uma forma geométrica clássica!
Occhialini era apenas um calouro quando Hancock o apresentou ao quebra-cabeça do fluoreto de escândio. Ele teve que aprender a matemática enquanto avançava, mas depois de cerca de dois semestres trabalhando nisso, ele descobriu a equação que descrevia o que estava acontecendo. Agora em seu último ano, ele diz que suas experiências de pesquisa no laboratório de Hancock foram essenciais para sua experiência como estudante de graduação.
A equação funciona lindamente e explica certos aspectos das medições experimentais de raios-X de Hancock também.
"Aprendi muito mais fazendo pesquisas do que qualquer curso poderia ter me proporcionado, "Diz Occhialini.