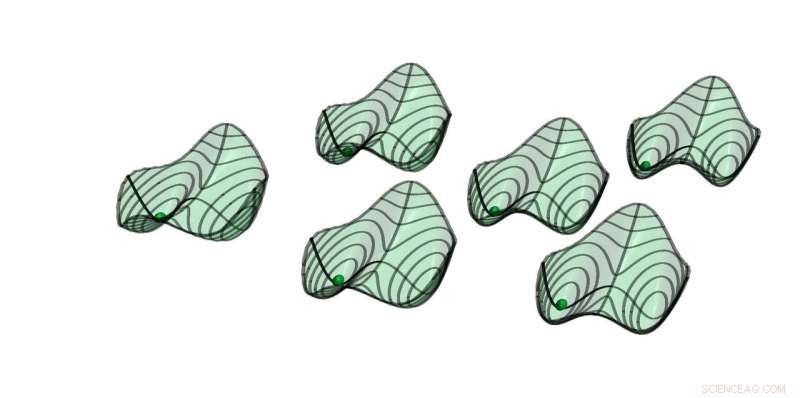
Quase potenciais de seis osciladores paramétricos com acoplamento all-to-all fraco. Soluções estáveis estão localizadas nos mínimos. As bolas indicam a solução simétrica, onde todos os osciladores estão em fase. (Captura de tela da animação que acompanha) Crédito:ETH Zurich / D-PHYS Toni Heugel
Estruturas conhecidas como cristais de tempo, que repetem no tempo da mesma forma que os cristais convencionais se repetem no espaço, recentemente capturou o interesse e a imaginação de pesquisadores de várias disciplinas. O conceito surgiu do contexto de sistemas quânticos de muitos corpos, mas os físicos da ETH desenvolveram agora uma estrutura versátil que esclarece conexões com trabalhos clássicos que datam de quase dois séculos, fornecendo assim uma plataforma unificadora para explorar fenômenos aparentemente diferentes.
Em um cristal, átomos são altamente ordenados, ocupando locais bem definidos que formam padrões espaciais. Sete anos atrás, o ganhador do Nobel de física em 2004, Frank Wilczek, ponderou a possibilidade de um análogo do tempo da ordem espacial cristalina - sistemas que exibem modulações temporais periódicas sustentadas em seu estado de energia mais baixa. O conceito de tais estruturas com um estado fundamental oscilante é altamente intrigante. Ai, não muito depois de a ideia ser publicada, foi provado que tais cristais de tempo não são possíveis sem quebrar as leis fundamentais da física. Contudo, o trabalho teórico subsequente sugeriu que, quando os sistemas quânticos de muitos corpos são acionados periodicamente, surgem novas correlações de tempo persistentes que evocam os cristais de tempo de Wilczek. Esses sistemas acionados foram chamados de cristais de tempo discreto, e em 2017, as primeiras realizações experimentais de tais estados foram relatadas em conjuntos de partículas acopladas (íons, elétrons e núcleos) que exibem propriedades de mecânica quântica.
Uma história não tão breve dos cristais do tempo
Muito antes, observadores astutos identificaram semelhanças distintas entre cristais de tempo discreto em sistemas quânticos e os chamados ressonadores paramétricos, um conceito na física clássica que remonta ao trabalho de Michael Faraday em 1831. A conexão entre esses dois corpos de trabalho permaneceu, Contudo, opaco. Agora, os teóricos desenvolveram uma nova estrutura que ajuda muito a eliminar as ambigüidades que cercam as semelhanças entre os sistemas clássicos e quânticos periodicamente conduzidos.
Escrevendo em artigo publicado hoje na revista Cartas de revisão física , Toni Heugel, um Ph.D. estudante do Departamento de Física da ETH Zurique, e Matthias Oscity, um aluno da mesma instituição, trabalhando com o Dr. Ramasubramanian Chitra e o Prof. Oded Zilberberg do Instituto de Física Teórica e com o Dr. Alexander Eichler do Laboratório de Física do Estado Sólido, relatar trabalho teórico e experimental que estabelece como cristais de tempo discreto podem ser gerados que, por um lado, não requerem efeitos mecânicos quânticos e, por outro lado, exibem efeitos genuínos de muitos corpos, que é uma característica de cristais de tempo discreto relatados em sistemas quânticos.
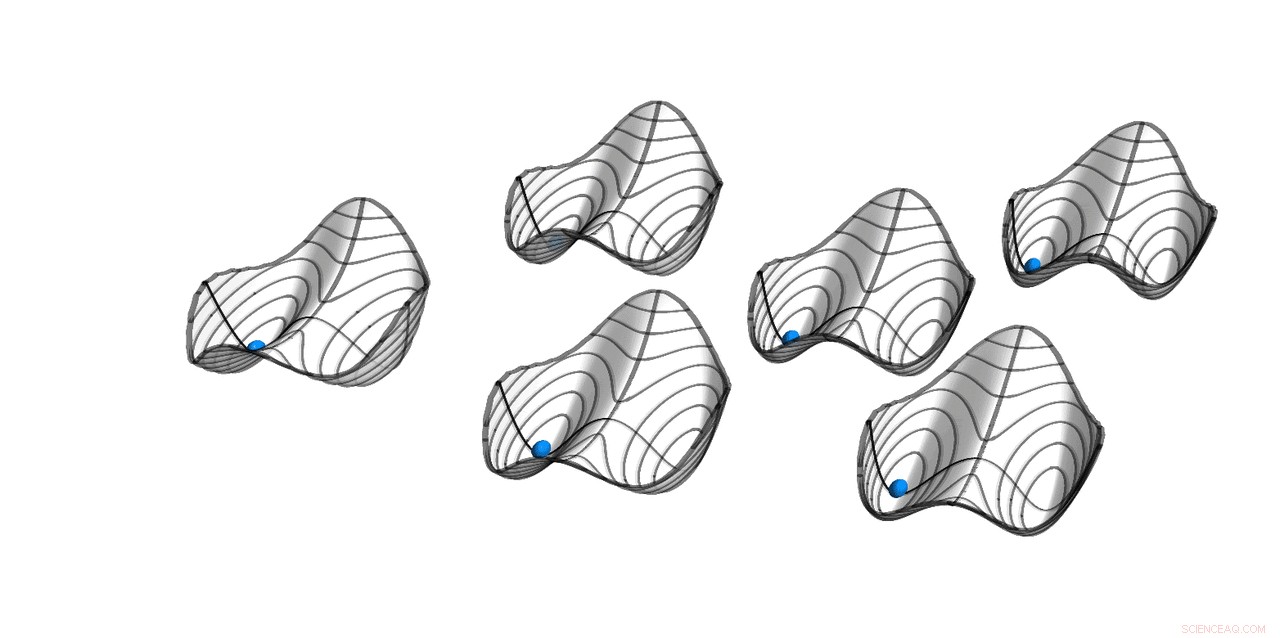
Quase potenciais de seis osciladores paramétricos com acoplamento all-to-all fraco. Soluções estáveis estão localizadas nos mínimos. As bolas indicam a solução simétrica, onde todos os osciladores estão em fase. O hamiltoniano H governa o movimento do sistema no período T, enquanto a própria solução tem período 2T. Essa quebra de simetria de translação de tempo discreto torna o sistema um cristal de tempo discreto. Crédito:ETH Zurich / D-PHYS Toni Heugel
Muitas maneiras de frequências subharmônicas
Há uma semelhança óbvia entre ressonadores paramétricos clássicos e cristais de tempo discretos realizados experimentalmente em sistemas quânticos de muitos corpos:ambos exibem dinâmica emergente em frequências que são frações da frequência de comando. No contexto de cristais de tempo discreto, o surgimento de oscilações em tais frequências sub-harmônicas quebra a periodicidade temporal do sistema acionado, fornecendo um 'análogo do tempo' à ordem espacial cristalina, em que a simetria do espaço é quebrada. Em sistemas clássicos de comando paramétrico, frequências sub-harmônicas aparecem de maneiras mais familiares:uma criança em um balanço, por exemplo, modifica o centro de gravidade com o dobro da frequência da oscilação resultante, ou o rabo de cavalo de um corredor oscila na metade da frequência do movimento vertical da cabeça.
Mas esses fenômenos diferentes têm algo a ver um com o outro? Sim, dizem os físicos da ETH. Em particular, eles identificam onde os aspectos de muitos corpos aparecem nos sistemas clássicos. Para fazer isso, eles consideraram osciladores não lineares clássicos com acoplamento ajustável entre eles.
Estrutura unificadora para sistemas clássicos e quânticos periodicamente conduzidos
É bem sabido que para certas frequências e intensidades de direção, osciladores paramétricos tornam-se instáveis e, em seguida, passam por uma chamada bifurcação de duplicação de período, além do qual eles oscilam na metade de sua freqüência de condução. Heugel, Oscity e seus colegas exploram o que acontece quando vários desses osciladores são acoplados. Em cálculos, bem como em experimentos usando duas cordas com acoplamento variável entre elas, eles encontram dois regimes distintos. Quando o acoplamento é forte, o sistema de duas cordas se move coletivamente, recriando em essência os movimentos da criança em um balanço ou no rabo de cavalo de um corredor. Contudo, no caso de acoplamento fraco entre as cordas, a dinâmica de cada corda é semelhante àquela exibida pelo sistema desacoplado. Como consequência, os osciladores acoplados não bifurcam coletivamente, mas bifurcam-se individualmente em parâmetros ligeiramente diferentes da unidade, levando a uma dinâmica geral mais rica, que se tornam cada vez mais complexos à medida que os sistemas ficam maiores.
Os pesquisadores da ETH argumentam que esses modos fracamente acoplados são semelhantes aos que emergem em sistemas quânticos de muitos corpos, implicando que sua estrutura pode explicar os comportamentos vistos experimentalmente nesses sistemas. Além disso, o novo trabalho prescreve condições gerais para a geração de cristais de tempo clássicos de muitos corpos. Em última análise, eles poderiam ser usados para interpretar e explorar características de seus equivalentes quânticos.
Tomados em conjunto, essas descobertas, portanto, fornecem uma estrutura unificadora poderosa para sistemas clássicos e quânticos periodicamente acionados exibindo dinâmica em frequências sub-harmônicas emergentes - sistemas que foram descritos até agora em contextos muito diferentes, mas pode não ser tão diferente assim.