Preso no meio:Bilhar com estrutura de memória leva a questões matemáticas

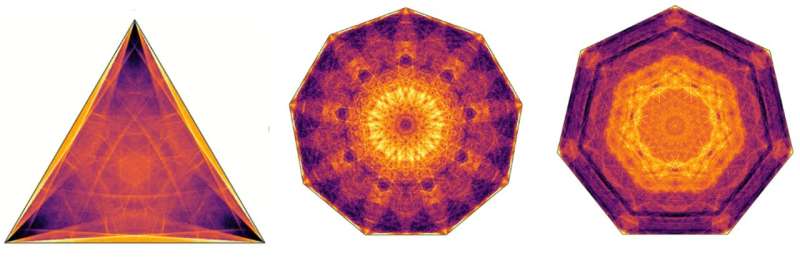Dependendo do formato do bilhar, a bola pode acabar ficando presa em locais diferentes com probabilidades diferentes. Esses "mapas de calor" mostram onde a bola tem maior probabilidade de acabar (cores brilhantes) e onde é menos provável que fique presa (cores escuras). Crédito:Cartas de revisão física (2024). DOI:10.1103/PhysRevLett.132.157101

Adicionar uma regra simples a um jogo de bilhar idealizado leva a uma riqueza de questões matemáticas intrigantes, bem como a aplicações na física dos organismos vivos. Esta semana, pesquisadores da Universidade de Amsterdã, incluindo dois estudantes de mestrado como primeiros autores, publicaram um artigo na Physical Review Letters sobre a fascinante dinâmica do bilhar com memória.

Uma versão idealizada do jogo de bilhar fascina os matemáticos há décadas. A questão básica é simples:depois que uma bola de bilhar é jogada, para onde ela vai e para onde vai? Suponha que o bilhar seja perfeito:as paredes saltam perfeitamente, não há outros objetos sobre a mesa, o movimento da bola é sem atrito e assim por diante. Então a bola realmente não “terminará” em lugar nenhum; continuará para sempre.

Mas será que alguma vez volta ao ponto de partida? Eventualmente ele visita todas as partes da mesa? Quando mudamos ligeiramente a direção da bola, ou a sua localização inicial, o caminho que ela segue se parece com o anterior?

Todas essas questões revelam-se muito intrigantes do ponto de vista matemático. Suas respostas nem sempre são conhecidas – especialmente quando o formato do bilhar não é simples, como um quadrado ou um retângulo. Por exemplo, no bilhar triangular com cantos inferiores a 100 graus, sabe-se que sempre existem caminhos periódicos – caminhos que a bola pode seguir e que retornam sobre si mesmos.

Isto pode ser provado matematicamente. Agora, mude um dos cantos para um ângulo um pouco maior e nenhum matemático saberá mais a resposta.

Os jogos idealizados de bilhar não são apenas o passatempo favorito dos matemáticos. Eles também têm um impacto profundo na física e em outras ciências. Muitas das questões sobre o bilhar podem ser formuladas como questões sobre o caos:condições iniciais semelhantes de um sistema dinâmico - seja uma bola em uma mesa de bilhar, uma molécula em um gás ou um pássaro em um bando - sempre levam a resultados finais semelhantes? resultados?

Uma nova regra

Numa investigação realizada na Universidade de Amesterdão, uma equipa de físicos percebeu que, ao alterar ligeiramente as regras do jogo de bilhar, o número de aplicações no mundo real aumenta ainda mais.

Mazi Jalaal, coautor da publicação e chefe do grupo onde foi realizada a pesquisa, explica:“Na natureza, muitos organismos vivos possuem uma forma externa de memória. Eles podem então usar essas informações para seguir a mesma rota novamente ou, por exemplo, ao procurar por comida, para não explorar a mesma região novamente.”

A última opção levou os investigadores a uma ideia interessante:e se adicionarmos uma regra ao jogo de bilhar, nomeadamente que a bola nunca pode cruzar o seu caminho anterior? O resultado é que o tamanho efetivo da mesa de bilhar fica cada vez menor. Na verdade, a bola acaba ficando presa em sua própria trajetória.

À medida que a bola se move pela mesa (linha vermelha), ela gradualmente 'corta' cada vez mais a área onde ela pode ir, deixando uma área permitida (azul) que fica cada vez menor. Eventualmente, a bola fica presa em um único ponto. Crédito:Mencione o artigo como fonte

Novas perguntas intrigantes

O efeito de captura torna o sistema ainda mais intrigante. Até mesmo perguntas simples tornam-se agora extremamente fascinantes. Qual a distância que uma bola percorre antes de ficar presa? A resposta varia, tanto no formato da mesa quanto no ponto de partida e na direção da bola.

Às vezes a bola percorre um comprimento que é apenas algumas vezes o tamanho da mesa, às vezes pode percorrer 100 vezes esse comprimento antes de ficar presa. Onde a bola eventualmente acaba presa também é uma questão complexa; repetir o experimento em um computador milhões de vezes, cada vez com posição inicial e velocidade ligeiramente diferentes, leva a belos padrões de configurações finais.

A imagem no topo deste texto mostra alguns desses belos exemplos. Curiosamente, os sistemas dinâmicos resultantes podem ser caóticos. Mudar apenas ligeiramente a posição inicial ou a velocidade da bola que se evita pode fazer com que ela fique presa em um ponto completamente diferente do bilhar.

Além disso, ao contrário do que acontece em uma mesa de bilhar comum, a bola que evita a si mesma não tem a mesma probabilidade de acabar em qualquer lugar. Algumas regiões são mais prováveis do que outras. Para explicar e provar todas essas características, os matemáticos certamente terão muito trabalho.

Aplicativos infinitos

Uma particularidade interessante da publicação é que ambos os seus primeiros autores são alunos de mestrado. Jalaal acrescenta:"A ideia de um 'bilhar com memória' é simples e nova o suficiente para estudá-lo não requer anos de experiência. Thijs e Stijn fizeram um ótimo trabalho ao tornar o material seu e encontrar maneiras inteligentes de estudar todos esses novos problemas em aberto. Estou muito feliz que eles já possam ser autores principais de uma publicação."

Os resultados são apenas os primeiros passos no que poderia ser uma área de pesquisa totalmente nova. Não só existem muitas questões matemáticas interessantes que aguardam agora para serem respondidas; as aplicações na física, incluindo a biofísica, também são infinitas.

Jalaal diz:"O conceito de armadilha implora para ser explorado, também em sistemas da vida real. Por exemplo, sabemos que fungos viscosos unicelulares usam caminhos que evitam a si próprios. Eles também ficam presos e o que acontece quando ou possuem mecanismos inteligentes para evitar que isso aconteça? Será que os utilizam para melhorar as estratégias de procura de alimentos?

“Os resultados nos ajudariam a compreender melhor esses sistemas biológicos e talvez até a incorporar as lições que aprendemos para otimizar esta forma de bilhar com memória para uso em robôs”.

Mais informações: Thijs Albers et al, Bilhar com Memória Espacial, Cartas de Revisão Física (2024). DOI:10.1103/PhysRevLett.132.157101. No arXiv :DOI:10.48550/arxiv.2307.01734
Informações do diário: Cartas de revisão física , arXiv

Fornecido pela Universidade de Amsterdã

Novos avanços prometem computação quântica segura em casa

Novo avanço tecnológico para imagens 3D rápidas e eficientes de objetos

Física