Cientistas e engenheiros de materiais gostariam de saber precisamente como os elétrons interagem e se movem em novos materiais e como os dispositivos feitos com eles se comportarão. A corrente elétrica fluirá facilmente dentro do material? Existe uma temperatura na qual o material se tornará supercondutor, permitindo que a corrente flua sem fonte de energia? Por quanto tempo o estado quântico do spin do elétron será preservado em novos dispositivos eletrônicos e quânticos?



Uma comunidade de físicos de materiais tenta resolver essas questões compreendendo o que acontece dentro dos materiais, calculando seu comportamento até o nível das interações individuais dos elétrons e dos movimentos atômicos.

Agora, uma equipe da Caltech fez uma descoberta importante que ajuda a simplificar esses cálculos, acelerando-os por um fator de 50 ou mais, mantendo a precisão. Como resultado, é possível calcular interações eletrônicas em materiais e dispositivos mais complexos, bem como desenvolver novos cálculos que antes eram considerados impossíveis.

Em um novo artigo publicado na revista Physical Review X , Yao Luo, da Caltech, estudante de pós-graduação em física aplicada; seu orientador Marco Bernardi, professor de física aplicada, física e ciência dos materiais; e colegas descrevem um novo método baseado em dados que permitiu esses avanços. Sua abordagem simplifica as densas matrizes computacionais usadas para representar as interações que ocorrem em um material entre elétrons e vibrações atômicas (ou fônons, que podem ser considerados unidades individuais de energia vibracional).

Luo e Bernardi afirmam que o novo método permite utilizar apenas 1 a 2% dos dados normalmente utilizados para resolver esses problemas, acelerando muito os cálculos e, no processo, revelando as interações mais importantes que ditam as propriedades dos materiais.

“Isso foi muito surpreendente”, diz Bernardi. "As interações elétron-fônon calculadas com as matrizes comprimidas são quase tão precisas quanto o cálculo completo. Isso reduz tremendamente o tempo de computação e o uso de memória, em cerca de duas ordens de grandeza na maioria dos casos. É também um exemplo elegante da navalha de Occam, a navalha de Occam. ideia de favorecer modelos físicos simples com um número mínimo de parâmetros."

Encontrando um novo meio-termo para a área

Os pesquisadores neste campo geralmente seguem uma de duas abordagens para compreender os materiais neste nível mais fundamental. Uma abordagem enfatiza a construção de modelos mínimos, reduzindo a complexidade do sistema, para que os pesquisadores possam ajustar alguns parâmetros em cálculos feitos com caneta e papel para obter uma compreensão qualitativa dos materiais.

O outro começa com nada mais do que a estrutura de um material e usa os chamados métodos de "primeiros princípios" - cálculos de mecânica quântica que exigem grandes computadores - para estudar as propriedades dos materiais com precisão quantitativa.

Este último conjunto de métodos, no qual o grupo de Bernardi se concentra, usa matrizes extremamente grandes com bilhões de entradas para calcular interações eletrônicas que controlam uma ampla gama de propriedades físicas. Isso se traduz em milhares de horas de computação para cada cálculo. O novo trabalho sugere uma espécie de meio-termo entre as duas abordagens, diz Bernardi.

"Com nosso novo método você pode truncar o tamanho dessas matrizes, extrair as principais informações e gerar modelos mínimos das interações nos materiais."

Erradicando os valores singulares mais importantes

A abordagem de seu grupo é baseada na aplicação de um método chamado decomposição de valores singulares (SVD) às interações elétron-fônon em um material. A técnica SVD é amplamente utilizada em áreas como compressão de imagens e ciência da informação quântica. Aqui, permite aos autores separar, ou desembaraçar, os componentes eletrônicos e vibracionais em uma matriz de milhares ou milhões de interações elétron-fônon e atribuir um número a cada interação fundamental.

Esses números reais positivos são chamados de valores singulares e classificam as interações fundamentais em ordem de importância. Então o programa pode eliminar todas as interações em cada matriz, exceto uma pequena porcentagem, deixando apenas os valores singulares iniciais, um processo que torna a determinação mais barata por um fator proporcional à quantidade de compactação.

Assim, por exemplo, se o programa mantiver apenas 1% dos valores singulares, o cálculo se tornará mais rápido por um fator de 100. Os pesquisadores descobriram que mantendo apenas uma pequena fração dos valores singulares, normalmente 1 a 2%, o resultado aproximado mantém quase a mesma precisão do cálculo completo.

“Ao usar SVD, você pode reduzir o número de valores singulares e capturar apenas as principais características das matrizes que representam interações eletrônicas em um determinado material”, diz Luo, autor principal do artigo e que está no terceiro ano no grupo de Bernardi.

"Isso trunca a matriz original, acelerando assim o algoritmo, e tem o benefício adicional de revelar quais interações no material são dominantes."

Bernardi observa que este último benefício do método SVD dá aos pesquisadores uma “intuição física” sobre as interações dos elétrons em um material, algo que faltou nos cálculos dos primeiros princípios no passado. Por exemplo, num cálculo envolvendo silício, ficou claro que o valor singular dominante estava associado ao estiramento e compressão de uma ligação específica.

“É algo simples, mas antes de fazer o cálculo não sabíamos qual era a interação mais forte”, explica Bernardi.

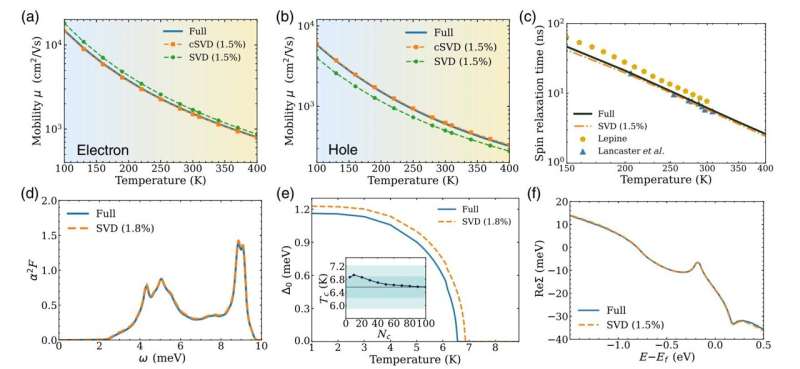
No artigo, os pesquisadores mostram que a compressão de matrizes relacionadas às interações elétron-fônon usando o método SVD fornece resultados precisos para várias propriedades de materiais que os pesquisadores podem querer calcular, incluindo transporte de carga, tempos de relaxamento de spin e temperatura de transição de supercondutores. .

Bernardi e sua equipe estão estendendo os cálculos baseados em SVD para uma gama mais ampla de interações em materiais e desenvolvendo cálculos avançados que antes eram considerados impossíveis. A equipe também está trabalhando para adicionar o novo método SVD ao código aberto Perturbo, um pacote de software que ajuda os pesquisadores a calcular como os elétrons interagem e se movem nos materiais. Bernardi diz que isso permitirá que os usuários da comunidade científica prevejam as propriedades dos materiais associadas às interações elétron-fônon de forma significativamente mais rápida.

O artigo é intitulado "Compressão baseada em dados de interações elétron-fônon". Junto com Luo e Bernardi, os coautores do artigo incluem o estudante de pós-graduação Dhruv Desai (MS '22); Benjamin Chang (MS '20) e Jinsoo Park (Ph.D. '22), que agora é pós-doutorado na Universidade de Chicago.