Inferir o tamanho de um coletivo de partículas Vicsek autopropulsadas a partir do movimento aleatório de uma única unidade
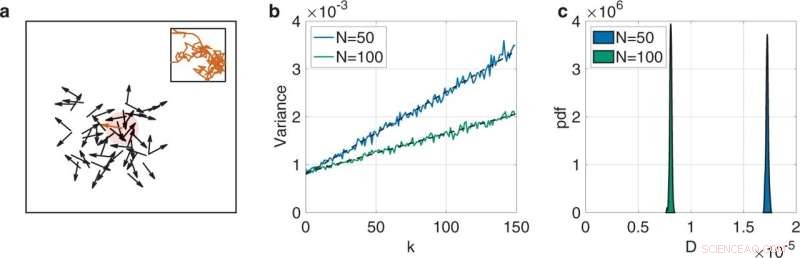
Ilustração da abordagem proposta para inferir o tamanho de um coletivo de partículas Vicsek autopropulsadas a partir do movimento de uma única unidade. Realizamos 1000 repetições onde registramos o cabeçalho de uma partícula no coletivo para diferentes valores do comprimento do lado L do domínio do quadrado, velocidade s, número de partículas N e ruído η. a Esquema de um experimento numérico para N = 20, onde exibimos um instantâneo de tempo do sistema (a partícula focal está em vermelho e seu círculo de interação está sombreado). A inserção mostra uma trajetória de amostra da partícula focal evoluindo do instantâneo por 150 etapas de tempo. b Variação Yk do cabeçalho da partícula focal em função do tempo k para dois tamanhos de sistema quando η = 0,1, s = 3 e L = 4, com as linhas pretas tracejadas marcando o ajuste linear. Dobrar o tamanho reduz pela metade o coeficiente de difusão (N = 50: D = 1,67 × 10
−5
e N = 100: D = 8,41 × 10
−6
). c Distribuição do coeficiente de difusão como seria estimado a partir de observações de diferentes partículas focais no coletivo. Crédito:Física das Comunicações (2022). DOI:10.1038/s42005-022-00864-9
A dinâmica coletiva é onipresente no mundo natural. De circuitos neurais a grupos de animais, existem inúmeros casos em que as interações entre um grande número de unidades elementares conferem padrões surpreendentemente complexos de beleza tentadora ao coletivo. Um dos objetivos de longa data dos pesquisadores em muitas áreas é entender os comportamentos de um grande grupo de unidades individuais, monitorando as ações de uma única unidade. Por exemplo, um ornitólogo pode aprender muitas coisas sobre o comportamento de um bando monitorando apenas uma única ave.
De maior dificuldade é entender o tamanho de uma coleção de unidades observando uma única unidade. Não importa quantas aves sejam marcadas com equipamento de monitoramento, nunca se pode ter certeza de ter marcado todo o bando. No entanto, embora a capacidade de calcular o tamanho de um coletivo a partir de comportamentos individuais seja uma ferramenta fundamental para qualquer campo, há apenas um punhado de artigos recentes tentando resolver o problema aparentemente insolúvel.
Em um estudo recém-publicado que aparece em
Communications Physics , pesquisadores liderados por Maurizio Porfiri, Professor do Instituto de Engenharia Mecânica e Aeroespacial e Engenharia Biomédica, e membro do Centro de Ciência e Progresso Urbano (CUSP) da Escola de Engenharia Tandon da NYU; e Pietro De Lellis, da Universidade de Nápoles, Itália, oferecem um paradigma para resolver esse problema, que se baseia em preceitos que podem ser rastreados até o trabalho de Einstein.
Ao observar um sistema de partículas autopropulsadas de Vicsek – uma conceituação matemática de movimento e enxame de partículas – como um modelo universal para dinâmica coletiva, eles mostram que a taxa de crescimento temporal da direção quadrada média de qualquer partícula é suficiente para prever a número de partículas no sistema sob parâmetros particulares, como uma temperatura conhecida e constante.
Em termos gerais, o estudo fornece um método rigoroso e matematicamente comprovado para inferir o tamanho de um coletivo realista a partir de medições de algumas de suas unidades, cujo movimento aleatório contém as pegadas de todo o sistema. Os fundamentos teóricos do método fornecem mais evidências para as analogias identificadas por Einstein entre a pesquisa interdisciplinar no comportamento coletivo de grupos de animais e a física moderna. Trabalhos futuros nessa linha podem estudar coletivos reais, de enxames de insetos a bandos de pássaros, cardumes de peixes e multidões humanas.
+ Explorar mais Um avanço na estimativa do tamanho de uma rede (principalmente oculta)
