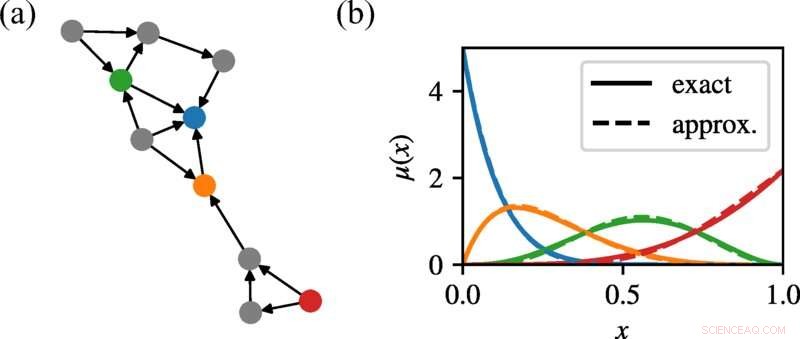
Em (a) mostramos uma rede de crescimento aleatório com grau de saída de Poisson. Em (b) mostramos os marginais posteriores para quatro nós representativos, coloridos para corresponder (a), comparando aqueles obtidos pelo nosso método com os resultados exatos da enumeração exaustiva. Apesar da presença de ciclos curtos, nossa abordagem de propagação de crenças se aproxima bastante das marginais, combinando não apenas as médias, mas as formas dessas distribuições. Crédito:Revisão Física E (2022). DOI:10.1103/PhysRevE.105.L052303
O mundo está repleto de classificações e ordenações. Eles aparecem no tênis – como no Aberto da França, que termina com uma classificação final dos jogadores campeões. Eles aparecem em pandemias – como quando as autoridades de saúde pública podem registrar novas infecções e usar o rastreamento de contatos para esboçar redes de disseminação do COVID-19. Sistemas de competição, conflito e contágio podem dar origem a hierarquias.
No entanto, essas hierarquias são observadas após o fato. Isso torna difícil saber os verdadeiros rankings do sistema:Quem foi realmente o melhor jogador? Quem infectou quem? "Você não pode voltar no tempo e aprender exatamente como isso aconteceu", diz o bolsista de pós-doutorado da SFI George Cantwell. Pode-se construir um modelo da rede e comparar todos os resultados possíveis, mas essa abordagem de força bruta rapidamente se torna insustentável. Se você estivesse tentando classificar algum grupo com apenas 60 participantes, por exemplo, o número de permutações possíveis atinge o número de partículas no universo conhecido.
Para um artigo recente publicado na
Physical Review E , Cantwell colaborou com o professor da SFI Cris Moore, cientista da computação e matemático, para descrever uma nova maneira de avaliar os rankings. Seu objetivo não era encontrar uma hierarquia verdadeira, mas calcular a dispersão de todas as hierarquias possíveis, com cada uma ponderada por sua probabilidade.
“Estávamos dispostos a não estar exatamente certos, mas queríamos obter boas respostas com algum senso de quão boas elas são”, diz Cantwell. O novo algoritmo é inspirado na física:as classificações são modeladas como entidades interativas que podem se mover para cima ou para baixo. Através dessa lente, o sistema se comporta como um sistema físico que pode ser analisado usando métodos da teoria do vidro de spin.
Logo após o início da pandemia do COVID-19, Cantwell e Moore começaram a pensar em modelos de como a doença se espalha por meio de uma rede. Eles rapidamente reconheceram a situação como um problema de ordenação que surge ao longo do tempo, não muito diferente da disseminação de um meme nas redes sociais ou do surgimento de rankings de campeonatos em esportes profissionais. "Como você ordena as coisas quando tem informações incompletas?" pergunta Cantwell.
Eles começaram imaginando uma função que poderia pontuar uma classificação de precisão. Por exemplo:Uma boa classificação seria aquela que concorda com os resultados dos confrontos 98% das vezes. Uma classificação que concorda com os resultados apenas 10% das vezes seria ruim – pior do que um cara ou coroa sem qualquer conhecimento prévio.
Um problema com os rankings é que eles são tipicamente discretos, o que significa que seguem os números inteiros:1, 2, 3 e assim por diante. Essa ordenação sugere que a "distância" entre o primeiro e o segundo membros classificados é a mesma que entre o segundo e o terceiro. Mas esse não é o caso, diz Cantwell. Os melhores jogadores de um jogo, em todo o mundo, estarão próximos em termos de habilidade, então a diferença entre os jogadores mais bem classificados pode ser mais próxima do que parece.
"Muitas vezes você vê que jogadores de classificação mais baixa podem vencer jogadores de classificação mais alta, e a única maneira de o modelo fazer sentido e ajustar os dados é esmagando todas as classificações", diz Cantwell.
Cantwell e Moore descreveram um sistema que avalia os rankings com base em um sistema de numeração contínuo. Um ranking poderia atribuir qualquer número real — número inteiro, fração, decimal infinitamente repetido — a um jogador na rede. "Os números contínuos são mais fáceis de trabalhar", diz Cantwell, e esses números contínuos ainda podem ser traduzidos de volta para classificações discretas.
Além disso, essa nova abordagem pode ser usada para prever algo sobre o futuro, como o resultado de um torneio de tênis, e também inferir algo sobre o passado, como como uma doença se espalhou. "Esses rankings podem nos dizer a ordem das equipes esportivas do melhor para o pior. Mas eles também podem nos dizer a ordem em que as pessoas de uma comunidade foram infectadas com uma doença", diz Moore. "Mesmo antes de seu pós-doutorado, George estava trabalhando nesse problema como forma de melhorar o rastreamento de contatos em uma epidemia. Assim como podemos prever qual time vencerá um jogo, podemos inferir qual de duas pessoas infectou a outra quando entraram em contato. um com o outro."
Em trabalhos futuros, os pesquisadores dizem que planejam investigar algumas das questões mais profundas que surgiram. Mais de uma classificação pode concordar com os dados, mas discordar radicalmente de outras classificações, por exemplo. Ou uma classificação que parece incorreta pode ter alta incerteza, mas não ser imprecisa. Cantwell diz que também quer comparar as previsões do modelo com os resultados de competições do mundo real. Em última análise, diz ele, o modelo pode ser usado para melhorar as previsões em uma ampla gama de sistemas que levam a classificações, de modelos de doenças infecciosas a apostas esportivas.
Cantwell diz que manterá seu dinheiro – por enquanto. "Não estou pronto para começar a apostar nisso", diz ele.
+ Explorar mais O algoritmo de 'propagação de crenças' pode descrever com precisão sistemas complexos em rede?
