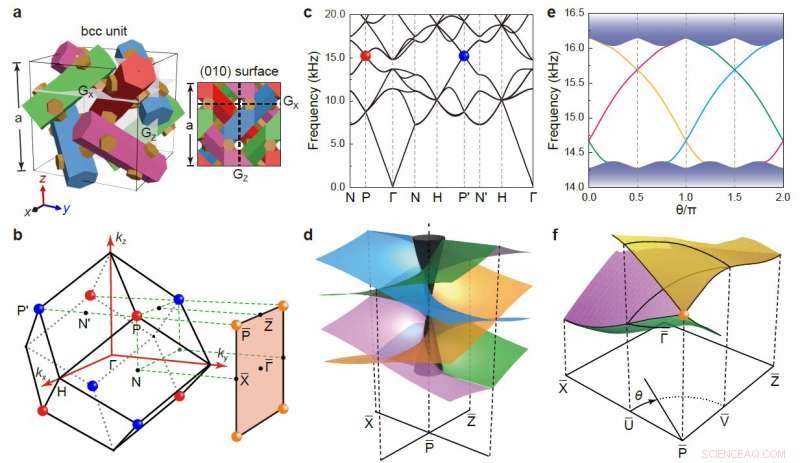
Esquema da unidade bcc (painel esquerdo) do cristal fonônico e sua (010) superfície (painel direito) caracterizada por dois espelhos deslizantes Gx e Gz. b, 3D bcc BZ e sua (010) superfície BZ. As esferas coloridas destacam os pontos principais de Dirac com igual frequência e suas projeções na superfície BZ. c, Bandas em massa simuladas ao longo de várias direções de alta simetria. d, Esquema das dispersões do estado de superfície quadri-helicoidal (superfícies coloridas), onde o cone cinza rotula a projeção dos estados em massa. e, Bandas de superfície simuladas ao longo de um loop de momento circular de raio 0,4π / a (como mostrado em f) centrado em P. As regiões de sombra indicam os estados em massa projetados. (f) gráfico 3D da dispersão de superfície simulada no primeiro quadrante da superfície BZ. As projeções da banda em massa não são mostradas para maior clareza. Crédito:BY Xiangxi Cai, Liping Ye, Chunyin Qiu, Meng Xiao, Rui Yu, Manzhu Ke, Zhengyou Liu
Semimetais Dirac são estados críticos de fases topologicamente distintas. Esses estados topológicos sem intervalos foram realizados por um mecanismo de inversão de banda, em que os pontos de Dirac podem ser aniquilados aos pares por perturbações sem alterar a simetria do sistema. Aqui, cientistas na China relatam uma observação experimental de pontos de Dirac que são reforçados completamente pela simetria do cristal usando um cristal fonônico não simórfico. Novos estados de superfície topológicos são demonstrados em seus experimentos.
A descoberta de novos estados topológicos da matéria tornou-se um objetivo vital na física fundamental e na ciência dos materiais. Um semimetal tridimensional (3-D) Dirac (DSM), acomodando muitas propriedades de transporte exóticas, como magnetorresistência anômala e mobilidade ultra-alta, é uma plataforma excepcional para explorar as transições de fase topológica e outros novos estados quânticos topológicos. É também de interesse fundamental servir como uma realização de estado sólido de um vácuo de Dirac (3 + 1) -dimensional. Até agora, os pontos de Dirac realizados vêm sempre aos pares e podem ser eliminados pela sua fusão e aniquilação aos pares, através da sintonização contínua dos parâmetros que preservam a simetria do sistema.
Em um novo artigo publicado em Ciência leve e aplicações , cientistas do Laboratório de Micro e Nanoestruturas Artificiais do Ministério da Educação e da Escola de Física e Tecnologia, Wuhan University, China, relatamos uma realização experimental de um cristal fonônico 3-D que hospeda pontos Dirac simétricos nos cantos da zona de Brillouin. Marcadamente diferente dos DSMs existentes, a ocorrência de pontos de Dirac é um resultado inevitável do grupo espacial não simórfico do material, que não pode ser removido sem alterar a simetria do cristal. Além dos pontos de Dirac identificados diretamente por medições de transmissão resolvidas em ângulo, estados superficiais quad-helicoides altamente intrincados são revelados por nossas medições de superfície e espectros de Fourier associados. Especificamente, os estados de superfície são compostos de quatro ramos espirais cruzados sem intervalos e, portanto, são notavelmente diferentes dos estados de superfície do arco de Fermi duplo observados recentemente em sistemas eletrônicos e fotônicos.
"Este estudo pode abrir novas maneiras de controlar o som, como perceber dispersão de som e radiação incomuns, considerando a dispersão cônica e a densidade de desaparecimento dos estados em torno dos pontos de Dirac. A dispersão em torno do ponto de Dirac é isotrópica, e assim, nosso sistema macroscópico serve como uma boa plataforma para simular a física relativística de Dirac, "os cientistas previram.