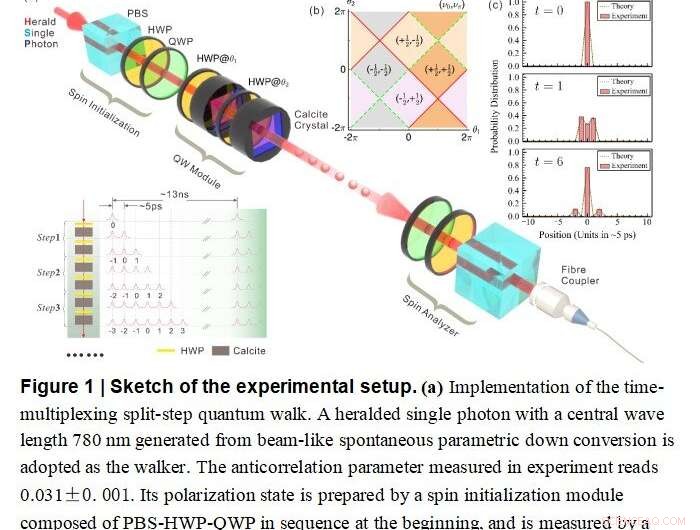
Esboço da configuração experimental Crédito:por Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei-Wei Pan, Zhe Chen, Munsif Jan, Kai Sun, Jin-Shi Xu, Yong-Jian Han, Chuan-Feng Li, Guang-Can Guo
Os processos dinâmicos de não equilíbrio são centrais em muitos contextos tecnológicos quânticos. Contudo, continua sendo um desafio fundamental identificar conceitos para sua caracterização e classificação, já que os estados quânticos resultantes desafiam propositalmente uma descrição em termos de física estatística de equilíbrio, a fim de realizar estados não acessíveis por meios convencionais. Os cientistas agora alcançaram uma caracterização em termos de um parâmetro de ordem topológica dinâmica para caminhadas quânticas, que representam uma classe paradigmática de processos de não-equilíbrio.
A coerência na dinâmica quântica está no cerne de fenômenos fascinantes além do reino da física clássica, como efeitos de interferência quântica, produção de emaranhamento e fases geométricas.
Os processos quânticos de natureza dinâmica inerente desafiam uma descrição em termos de um conjunto de física estatística de equilíbrio. Até agora, identificar os princípios gerais por trás da dinâmica quântica unitária subjacente que preservam a coerência quântica continua a ser um desafio chave.
Caminhadas quânticas fornecem uma plataforma poderosa e flexível para realizar experimentalmente e sondar a evolução do tempo quântico coerente longe do equilíbrio térmico. Ao contrário dos passeios aleatórios clássicos, caminhadas quânticas são caracterizadas por superposições quânticas de amplitudes, em vez de distribuições de probabilidade clássicas. Este caráter quântico genuíno já foi aproveitado em vários campos da física, variando do projeto de algoritmos eficientes no processamento de informações quânticas, observação de dinâmica correlacionada e localização de Anderson, à realização de fenômenos físicos exóticos nas fases topológicas do contexto.
Embora a ordem topológica possa ser recuperada no espaço real, acessar a informação completa de amplitude complexa que caracteriza a superposição coerente permanece como um dos principais desafios em experimentos de caminhada quântica.
Em um novo artigo publicado em Ciência leve e aplicação , cientistas do CAS Key Laboratory of Quantum Information e colaboradores internacionais relataram a observação direta de um parâmetro de ordem topológica dinâmica (DTOP) que fornece uma caracterização dinâmica de caminhadas quânticas.
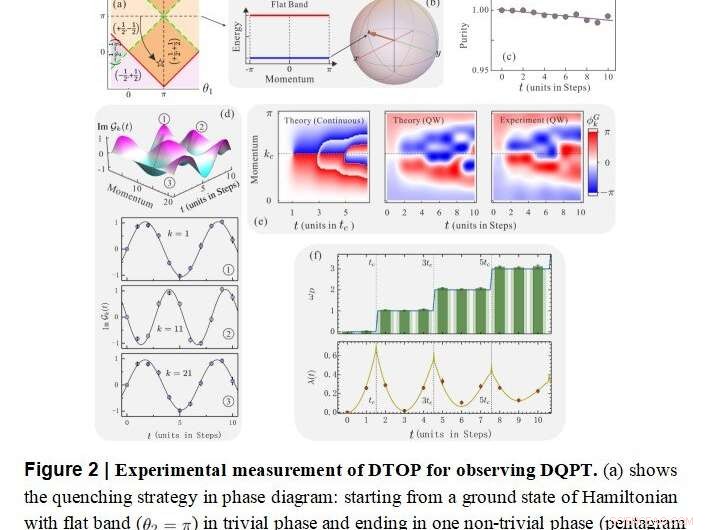
Medição experimental de DTOP para observar DQPT Crédito:por Xiao-Ye Xu, Qin-Qin Wang, Markus Heyl, Jan Carl Budich, Wei-Wei Pan, Zhe Chen, Munsif Jan, Kai Sun, Jin-Shi Xu, Yong-Jian Han, Chuan-Feng Li, Guang-Can Guo
Para este fim, eles realizaram uma caminhada quântica em etapas divididas em um sistema fotônico usando a estrutura da multiplexação no tempo. Usando uma técnica desenvolvida anteriormente, eles alcançaram tomografia de estado completo do estado quântico evoluído no tempo por até 10 etapas de tempo completas. Mais importante, isso forneceu todas as informações de amplitude complexa do estado de caminhada quântica.
"Isso é essencial para o nosso objetivo central de uma classificação dinâmica da caminhada quântica usando o DTOP, uma vez que o DTOP mede o número do enrolamento de fase ω_D (t) no espaço de momento, nomeadamente da chamada fase geométrica Pancharatnam (PGP) ".
A partir dos resultados experimentais, eles descobriram que as transições dinâmicas entre classes topologicamente distintas de caminhadas quânticas podem ser distinguidas exclusivamente pelo comportamento dependente do tempo observado de ω_D (t).
"Para uma têmpera entre dois sistemas com o mesmo caráter topológico, encontramos ω_D (t) =0 para todos os intervalos de tempo; em vez de, para uma têmpera entre dois sistemas topologicamente diferentes, ω_D (t) também começa em ω_D (t =0) =0, mas muda monotonamente seu valor em certos momentos críticos, "acrescentaram.
Generalizando essas observações, eles estabeleceram ainda uma relação única entre o comportamento de ω_D (t) e a mudança ao longo de um parâmetro de extinção nas propriedades topológicas de um hamiltoniano de Floquet eficaz que descreve estroboscopicamente a caminhada quântica.
Os cientistas concluem:"Desta forma, nós fornecemos uma perspectiva de não-equilíbrio para caminhadas quânticas, que pode ser entendido como um ponto de partida para abordar processos dependentes do tempo de um ângulo inerentemente dinâmico que vai além da noção de física estatística de equilíbrio. Com isso e o mapeamento em quenches em um sistema quântico equivalente de muitos corpos, nosso experimento oferece uma plataforma versátil para estudar a dinâmica coerente de não-equilíbrio de muitos modelos paradigmáticos, como o modelo Su-Schrieffer-Heeger, a cadeia de Kitaev da onda p, ou o modelo de Ising de campo transversal no futuro. "