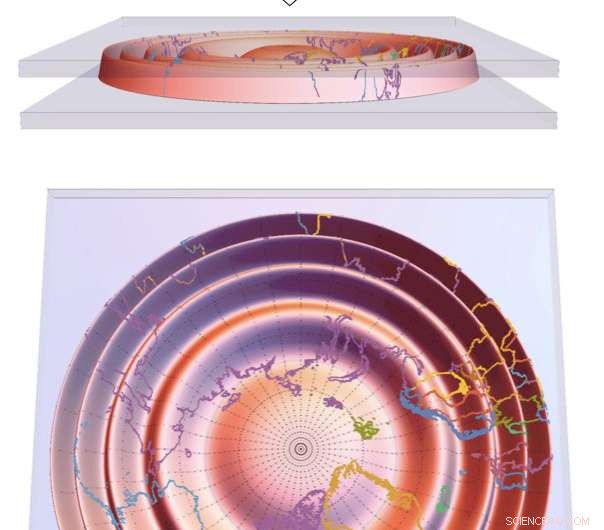
Este esquema mostra o que acontece quando uma concha elástica curva, aqui representado como um globo, é forçado pelo confinamento a mudar de esférico para plano. Se enrugar o suficiente, a casca pode se achatar quase sem esticar. A imagem inferior mostra que a distorção de distância introduzida ao achatar um globo - em comparação com um mapa pré-esmagado - pode ser arbitrariamente menor à medida que a casca se torna mais fina e mais flexível. Esta solução, desenvolvido por pesquisadores da UMass Amherst, reconcilia princípios básicos e aparentemente contraditórios de geometria e mecânica. Crédito:UMass Amherst / G. Grason
Abordando um problema de física que remonta a Galileu, três pesquisadores da Universidade de Massachusetts Amherst esta semana propõem uma nova abordagem para a teoria de como folhas finas podem ser forçadas a se conformar a formas "geometricamente incompatíveis" - pense em embrulhar uma bola de basquete para presente - que depende da combinação de duas ideias fundamentais de geometria e mecânica que por muito tempo foram considerados irreconciliáveis.
O físico teórico Benny Davidovitch, o cientista de polímeros Greg Grason e o estudante de doutorado Yiwei Sun, escrevendo em Proceedings of the National Academy of Sciences , sugerir e demonstrar por meio de simulações numéricas que folhas naturalmente planas forçadas a mudar sua curvatura podem acomodar a tensão geometricamente exigida, desenvolvendo rugas microscópicas que dobram a folha em vez de esticá-la até o ponto de ruptura, uma solução que custa menos energia, também.
Este avanço é importante à medida que os biotecnólogos tentam cada vez mais controlar o nível de tensão encontrado em filmes finos em conformidade com o complexo, formas curvas e 3D do corpo humano, por exemplo, em sensores flexíveis e usáveis para monitoramento de saúde personalizado, eles explicam. Muitos desses dispositivos dependem das propriedades elétricas do filme, que se mostra altamente vulnerável ao alongamento, mas que pode tolerar alguma curvatura.
O novo conceito é "perto o suficiente, "Davidovitch diz - as não conformidades que vêm com a dobra são tão pequenas que, em termos práticos, eles quase não custam energia. "Ao oferecer estratégias eficientes para controlar a cepa, prever e controlar, oferecemos uma nova ferramenta quantitativa que é útil para pessoas que prevêem as forças necessárias para gravar ou embrulhar folhas finas nanoscópicas e cascas em substratos de diferentes formatos, "eles afirmam.
Ele adiciona, "Nosso trabalho mostra que, ao permitir pequenas rugas na embalagem, a quantidade necessária de alongamento cai drasticamente. Para um invólucro extremamente fino, como o disponível hoje em laboratórios, o alongamento pode ser eliminado quase totalmente. "
Grason aponta, "Nossa estrutura teórica fornece uma ferramenta simples e adaptável para a compreensão de como controlar e manipular, e idealmente para otimizar, o nível de tensão que uma dada geometria impõe a tal dispositivo, e, assim, melhorar seu desempenho. "
Davidovitch diz que existem dois tipos de cientistas interessados neste problema de longa data, um menos motivado pela praticidade do que por como as leis da Natureza se aplicam. Esses pensadores estão familiarizados com "o feixe de Galileu, "um problema de mecânica / física que imaginava uma viga saindo de uma parede de pedra que se dobraria ou deformará quando o peso fosse adicionado a ela, ele observa. Prever as forças e a tensão sobre ele representou um quebra-cabeça de longa data.
Galileo não resolveu o quanto o feixe se deformará ou como prever isso, ele observa, mas esse problema relacionado à deformação foi posteriormente explorado e definido por meio de novas abordagens da geometria de objetos contínuos pelo matemático e físico alemão Carl Friedrich Gauss. Físicos e matemáticos "concentraram muita atividade intelectual nisso ao longo dos séculos, "Davidovitch diz.
Depois de Galileu, Davidovitch disse, O matemático suíço Leonhard Euler desenvolveu a "teoria da elástica, "que argumenta que objetos confinados se dobram para evitar tensão, isso é, qualquer mudança no comprimento. Euler mostrou que uma situação em que absolutamente nenhum alongamento ocorre pode ocorrer em circunstâncias especiais, mas não no tipo geral de confinamento definido pelas restrições geométricas de Gauss, ele adiciona.
A nova ferramenta da equipe UMass Amherst mostra - quando uma restrição não pode ser perfeitamente satisfeita, mas quase satisfeita - como encontrar o estado físico ou a forma mais adequada. "É um novo ramo do cálculo variacional, "Davidovitch diz." Tudo que eu preciso fazer é minimizar a curvatura que quase elimina todo o alongamento, e me permite encontrar aquele com a menor energia de dobra possível. "
Eles propõem um novo princípio, a elástica de Gauss-Euler, que reconcilia as duas pedras angulares da mecânica clássica e da geometria definidas anteriormente pelas obras de Euler e Gauss. Eles invocam um novo regime de soluções das morfologias complexas dos corpos delgados, um problema de intenso interesse recente de biofísica e engenharia de materiais à matemática aplicada, Grason aponta.
Ele lembra, "Quando iniciamos esta linha de pesquisa, não imaginávamos como seria. Não estávamos tentando resolver esse problema. "Mas a estudante de doutorado Sun, executando algumas simulações de computador, apresentou resultados que desafiavam as suposições ingênuas de que o confinamento requer mais energia para esticar do que dobrar o lençol. As fórmulas que ele e Grason propuseram eram "impossíveis, "Davidovitch diz, "eles pareciam estar violando teoremas geométricos fundamentais."
Eles ficaram presos por dois anos, até que se lembraram do feixe de Galileu, o que Davidovitch chama de "contradição de pensamento, "que reformulou a questão. Foi" muito satisfatório "trazer uma nova ferramenta conceitual para o problema que não estava disponível antes, ele diz. Grason acrescenta, "É ótimo saber por que nossas simulações iniciais se comportaram de maneira tão estranha, claro. Mas, eventualmente, isso nos leva a entender melhor a questão, e como ele aborda uma classe muito mais ampla de problemas de uma nova maneira. Sim, isso dá uma sensação boa. "