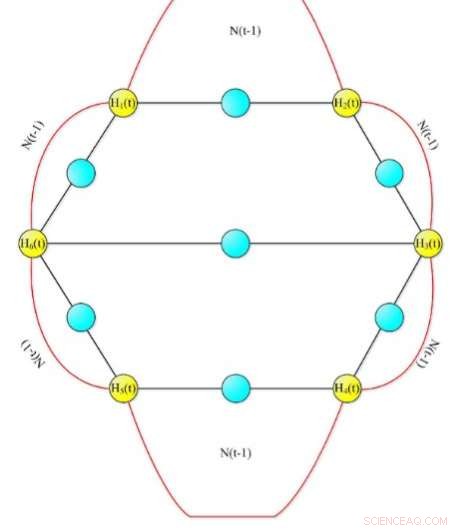
Diagrama do modelo de rede aleatório. Crédito:Springer
As redes são frequentemente descritas como árvores com ramos abrangentes. Como a árvore se ramifica depende da lógica por trás da expansão da rede, como a expansão aleatória. Contudo, alguns aspectos de tais redes em expansão aleatória são invariantes; em outras palavras, eles exibem as mesmas características, independentemente da escala da rede. Como resultado, toda a rede tem a mesma forma de uma ou mais de suas partes.
Em um novo estudo publicado em EPJ B , Fei Ma da Northwest Normal University em Lanzhou, Província de Gansu, China, e colegas calculam o número total de árvores abrangentes em redes que se expandem aleatoriamente. Este método pode ser aplicado para modelar modelos de rede sem escala, que, ao que parece, são caracterizados por propriedades de pequeno mundo. Isso significa, por exemplo, que os membros da rede exibem apenas seis graus de separação, como a maioria das pessoas em nossa sociedade.
Anteriormente, vários modelos de rede foram baseados em grafos que consistem em uma agregação de vértices com arestas de conexão. Mas eles não foram suficientes para modelar redes da vida real, como redes de usuários de mídia social. Em vez de, redes complexas, onde a rede é criada aleatoriamente, tornaram-se os pilares da ciência da computação e da matemática discreta moderna. Usando dados de redes da vida real, e aproveitando a experiência adquirida com redes artificiais criadas para dar conta de funções específicas, os autores projetam modelos mais realistas que são mais complexos do que seus predecessores.
Neste estudo, os autores se concentram no desenvolvimento de um método recursivo para calcular o número de árvores abrangentes em uma rede, o que é particularmente útil para prever sua capacidade de tolerar falhas que ocorrem aleatoriamente. Ser capaz de encontrar o número de árvores abrangentes em modelos de rede tem implicações para vários campos científicos, como matemática aplicada, ciência da computação teórica, física e Quimica.