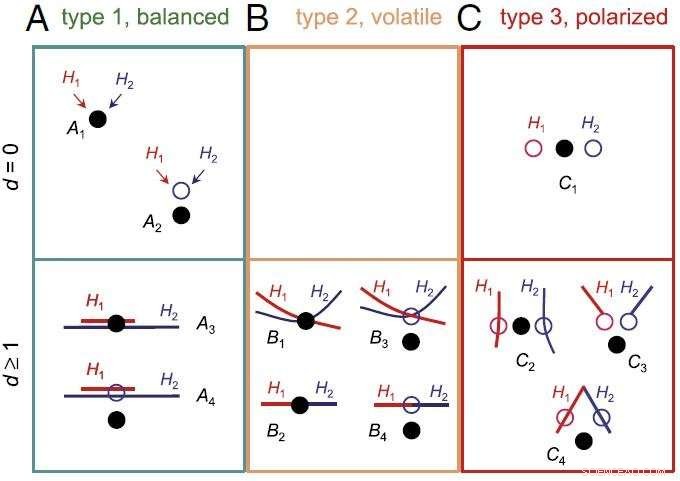
Classificação de problemas de seleção de modelos bayesianos envolvendo dois modelos igualmente certos ou igualmente errados. Crédito:ZHU Tianqi
Cientistas da University College London (UCL) e da Academy of Mathematics and Systems Science, Academia Chinesa de Ciências (CAS, AMSS), relataram progresso na compreensão de problemas associados à seleção de modelos bayesianos. A pesquisa sugere que o método bayesiano tende a produzir probabilidades posteriores muito altas para árvores evolutivas estimadas, mesmo se as árvores estiverem claramente erradas, e oferece uma possível explicação para esse fenômeno.
A comparação de modelos é amplamente usada em vários ramos das ciências em que hipóteses científicas são formuladas como modelos estatísticos e testadas usando dados observados. Contudo, a comparação de modelos é uma questão espinhosa tanto na estatística clássica quanto na estatística bayesiana.
Na estatística clássica, dois modelos aninhados são comparados. A estrutura não funciona quando os modelos comparados não estão aninhados. Em contraste, A estatística bayesiana compara diferentes modelos calculando suas probabilidades posteriores, o que indica nossa confiança ou crença no modelo.
As duas metodologias não surgem apenas de filosofias drasticamente diferentes, eles também podem produzir conclusões opostas na análise dos mesmos dados. A seleção do modelo bayesiano é conhecida por convergir para o modelo verdadeiro se o modelo verdadeiro for incluído entre os modelos em consideração.
Isso é, quando os cientistas coletam mais dados, a probabilidade posterior para o modelo certo aumentará e se aproximará de 100 por cento, e assim eles terão cada vez mais certeza de qual é o verdadeiro modelo.
Contudo, se todos os modelos considerados estiverem errados, o comportamento do método bayesiano é desconhecido.
Os cientistas caracterizaram problemas de seleção de modelos bayesianos, e os categorizou em três tipos, cada um dos quais mostra um comportamento diferente.
No caso mais cientificamente interessante, ou seja, quando os modelos comparados são distintos e quase igualmente errados, A seleção do modelo bayesiano mostra um comportamento polarizado problemático:tende a suportar um modelo com força total em alguns conjuntos de dados, mas suporta outro modelo em outros conjuntos de dados.
O resultado pode ser resumido usando a seguinte analogia:Suponha que o mundo seja cinza, mas perguntamos a um sábio se é preto ou branco. Ele dá uma olhada profunda no mundo e diz que é preto, com total confiança. Mas da próxima vez que fizermos a mesma pergunta, ele diz que é branco, novamente com total confiança.
Este estudo foi motivado por problemas em filogenética molecular, que é a ciência de trabalhar as relações entre as espécies usando dados genéticos, representado por árvores evolucionárias.
Essas diferentes árvores são modelos estatísticos opostos na análise bayesiana dos dados. Os biólogos evolucionistas observaram por muito tempo que o método tende a produzir probabilidades posteriores muito altas para as árvores evolutivas estimadas (muitas vezes 100 por cento), mesmo que as árvores estejam claramente erradas.
Nossos resultados fornecem uma possível explicação para esse comportamento desagradável. As implicações dos resultados para o uso da seleção de modelos bayesianos no teste de hipóteses científicas opostas em geral ainda precisam ser exploradas.