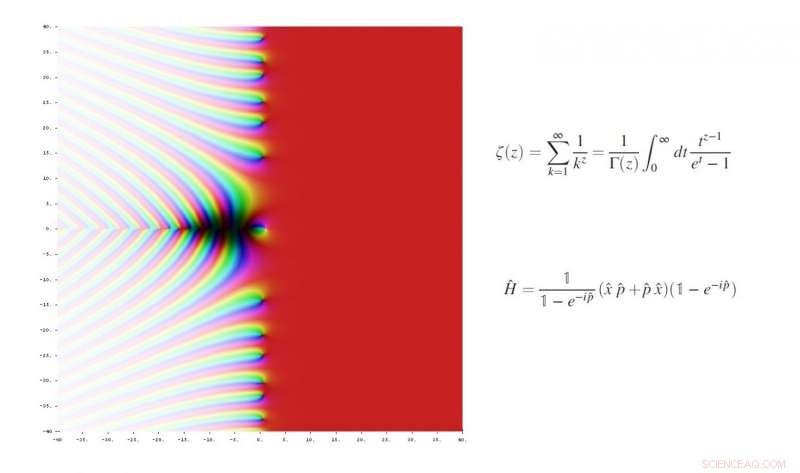
Em 1859, Riemann formulou a hipótese de que os zeros não triviais da função zeta de Riemann estão na linha vertical (½ + it) no plano complexo, em que a parte real é sempre ½. Crédito:Jan Homann, Wikimedia Commons. Acima:função zeta de Riemann. Parte inferior:a nova função do operador.
(Phys.org) —Os pesquisadores descobriram que as soluções para uma famosa função matemática chamada função zeta de Riemann correspondem às soluções de outra, tipo de função diferente que pode facilitar a resolução de um dos maiores problemas da matemática:a hipótese de Riemann. Se os resultados puderem ser verificados com rigor, então finalmente provaria a hipótese de Riemann, que vale $ 1, 000, Prêmio 000 Millennium do Clay Mathematics Institute.
Embora a hipótese de Riemann remonta a 1859, nos últimos 100 anos ou mais, os matemáticos têm tentado encontrar uma função de operador como a descoberta aqui, pois é considerada uma etapa fundamental da prova.
"Para nosso conhecimento, esta é a primeira vez que um operador explícito - e talvez surpreendentemente relativamente simples - foi identificado cujos autovalores ['soluções' na terminologia da matriz] correspondem exatamente aos zeros não triviais da função zeta de Riemann, "Dorje Brody, um físico matemático da Brunel University London e co-autor do novo estudo, contado Phys.org .
O que ainda precisa ser provado é a segunda etapa-chave:que todos os autovalores são números reais em vez de imaginários. Se o trabalho futuro pode provar isso, então finalmente provaria a hipótese de Riemann.
Brody e seus co-autores, os físicos matemáticos Carl Bender da Washington University em St. Louis e Markus Müller da University of Western Ontario, publicaram seu trabalho em uma edição recente da Cartas de revisão física .
Espaçamento de primos
A hipótese de Riemann tem um forte fascínio porque está profundamente ligada à teoria dos números e, em particular, os números primos. Em seu artigo de 1859, O matemático alemão Bernhard Riemann investigou a distribuição dos números primos - ou mais precisamente, o problema "dado um número inteiro N, quantos números primos existem que são menores do que N? "
Riemann conjecturou que a distribuição dos números primos menores do que N está relacionada aos zeros não triviais do que agora é chamado de função zeta de Riemann, ζ ( s ) (Os zeros são as soluções, ou os valores de s que tornam a função igual a zero. Embora fosse fácil para os matemáticos ver que havia zeros sempre s é um número par negativo, esses zeros são considerados zeros triviais e não são a parte interessante da função.)
A hipótese de Riemann era que todos os zeros não triviais estão ao longo de uma única linha vertical (½ + isto ) no plano complexo - o que significa que seu componente real é sempre ½, enquanto seu componente imaginário eu varia conforme você sobe e desce na linha.
Nos últimos 150 anos, matemáticos encontraram literalmente trilhões de zeros não triviais, e todos eles têm um componente real de ½, exatamente como Riemann pensava. É amplamente aceito que a hipótese de Riemann é verdadeira, e muito trabalho foi feito com base nessa suposição. Mas apesar dos esforços intensos, a hipótese de Riemann - de que todos os infinitos zeros estão nesta única linha - ainda não foi provada.
Soluções idênticas
Uma das pistas mais úteis para provar a hipótese de Riemann veio da teoria das funções, que revela que os valores da parte imaginária, t , em que a função desaparece são números discretos. Isso sugere que os zeros não triviais formam um conjunto de números reais e discretos, que é como os valores próprios de outra função chamada de operador diferencial, que é amplamente utilizado na física.
No início dos anos 1900, essa semelhança levou alguns matemáticos a se perguntar se realmente existe um operador diferencial cujos autovalores correspondem exatamente aos zeros não triviais da função zeta de Riemann. Hoje essa ideia é chamada de conjectura de Hilbert-Pólya, nomeado em homenagem a David Hilbert e George Pólya - apesar do fato de nenhum deles publicou nada sobre isso.
"Como não há publicação de Hilbert ou Pólya, a declaração exata do programa Hilbert-Pólya está sujeita, até certo ponto, a interpretação, mas provavelmente não é irracional dizer que consiste em duas etapas:(a) encontre um operador cujos autovalores correspondam aos zeros não triviais da função zeta de Riemann; e (b) determinar se os valores próprios são reais, "Brody disse.
"O foco principal do nosso trabalho até agora foi na etapa (a), "ele disse." Nós identificamos um operador cujos autovalores correspondem exatamente aos zeros não triviais da função zeta de Riemann. Estamos apenas começando a pensar sobre a etapa (b), e de fato como enfrentar este desafio. Se será difícil ou fácil preencher as etapas que faltam em direção à etapa (b), a essa altura, não podemos especular - é necessário mais trabalho para ter uma ideia melhor da escala de dificuldade envolvida. "
O operador
Uma das coisas interessantes sobre o operador recém-descoberto é que ele tem laços estreitos com a física quântica.
Em 1999, quando os físicos matemáticos Michael Berry e Jonathan Keating estavam investigando a conjectura de Hilbert-Pólya, eles fizeram outra conjectura importante. Se tal operador existir, eles disseram, então deve corresponder a um sistema quântico teórico com propriedades particulares. Isso agora é chamado de conjectura de Berry-Keating. Mas ninguém jamais encontrou um sistema assim antes, e este é um segundo aspecto importante do novo trabalho.
"Identificamos uma condição de quantização para o hamiltoniano de Berry-Keating, assim, verificando essencialmente a validade da conjectura de Berry-Keating, "Brody disse.
Os hamiltonianos são freqüentemente usados para descrever a energia dos sistemas físicos. A nova operadora, Contudo, não parece descrever nenhum sistema físico, mas é antes uma função puramente matemática.
"Pode ser decepcionante, mas tal hamiltoniano não parece representar sistemas físicos de nenhuma maneira óbvia; ou pelo menos até agora não encontramos nenhuma indicação de que nosso hamiltoniano corresponda a qualquer sistema físico, "Brody disse.
"Mas pode-se perguntar 'por que publicar em PRL ? ' A resposta é porque muitas das técnicas usadas para algumas análises heurísticas em nosso artigo que são sugestivas são emprestadas de técnicas da teoria quântica simétrica PT pseudo-Hermitiana desenvolvida ao longo dos últimos 15 anos ou mais. O entendimento convencional da conjectura de Hilbert-Pólya é que o operador (hamiltoniano) deve ser hermitiano, e naturalmente se liga isso à teoria quântica, segundo a qual os hamiltonianos são convencionalmente exigidos como hermitianos. Estamos propondo uma forma pseudo-hermitiana do programa Hilbert-Pólya, que para nós parece valer a pena explorar mais. "
Soluções reais
Agora, o maior desafio que resta é mostrar que os autovalores do operador são números reais.
Em geral, os pesquisadores estão otimistas de que os valores próprios são realmente reais, e em seu artigo eles apresentam um forte argumento para isso com base na simetria PT, um conceito da física quântica. Basicamente, A simetria PT diz que você pode mudar os sinais de todos os quatro componentes do espaço-tempo (três dimensões de espaço ou "paridade" e uma dimensão de tempo), e, se o sistema for simétrico PT, então o resultado terá a mesma aparência do original.
Embora a natureza em geral não seja PT-simétrica, o operador que os físicos construíram é. Mas agora os pesquisadores querem mostrar que essa simetria é quebrada. Como eles explicam em seu artigo, se puder ser mostrado que a simetria PT é quebrada para a parte imaginária do operador, então, seguir-se-ia que os valores próprios são todos números reais, o que acabaria por constituir a prova tão esperada da hipótese de Riemann.
É geralmente considerado que uma prova da hipótese de Riemann será muito útil na ciência da computação, especialmente criptografia. Os pesquisadores também querem determinar o que seus resultados podem realmente significar para a compreensão de princípios matemáticos mais fundamentais.
"O que exploramos até agora contém poucos insights da teoria dos números; embora se possa esperar que, dada a sua importância na teoria dos números, certamente qualquer tentativa que faça progresso com sucesso no estabelecimento da hipótese de Riemann ofereceria insights da teoria dos números, "Brody disse." Claro que este não precisa ser o caso, mas, no entanto, seria interessante explorar se algum dos aspectos dinâmicos do sistema hipotético descrito por nosso hamiltoniano pode estar ligado a certos resultados teóricos dos números. A respeito disso, a análise semi-clássica em nosso hamiltoniano seria um dos próximos objetivos. "
© 2017 Phys.org