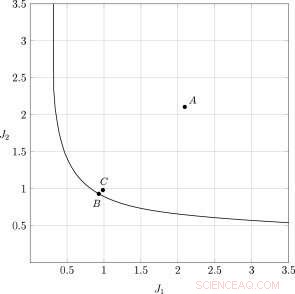
Uma frente ideal de pareto para sistema de grau único de liberdade. Crédito:Universidade Lobachevsky
Hoje em dia, as palavras "incerteza" e "multicritério" caracterizam da melhor maneira a relevância e a complexidade dos problemas modernos de gerenciamento de uma variedade de objetos e processos dinâmicos.
Na verdade, qualquer modelo matemático que descreve processos controlados complexos inevitavelmente inclui imprecisões na descrição de distúrbios existentes e parâmetros do objeto sob controle. Ignorar tal "incerteza" freqüentemente leva a erros fatais no funcionamento de sistemas de gestão reais. Por outro lado, os diferentes requisitos para o sistema de gestão são geralmente contraditórios. Isso leva à elaboração de tarefas multicritério, que, no caso de uma solução bem-sucedida, permita a exclusão de pelo menos soluções "ineficientes" conhecidas.
É bem sabido que as tarefas de gerenciamento de vários critérios são muito difíceis de executar. Essas dificuldades muitas vezes se ampliam devido à incerteza no cenário dos distúrbios atuais. Assim, o desenvolvimento da teoria e dos métodos de resolução desses problemas parece ser relevante tanto nos aspectos teóricos quanto aplicados.
Segundo o professor do Instituto de Tecnologias da Informação, Matemática e Mecânica Dr. Dmitry V. Balandin, o objeto de estudo é um sistema de equações diferenciais ordinárias ou equações diferenciais parciais. Supõe-se que um objeto dinâmico está sujeito a influência externa, com respeito ao qual se sabe apenas que pertence a uma dada classe. Além disso, as condições iniciais para o sistema em consideração também são consideradas desconhecidas e pertencentes a um determinado conjunto.
“Os indicadores que caracterizam os transitórios para toda a classe de influências externas e condições iniciais, chamados desvios máximos das saídas do sistema, são introduzidos para o sistema em consideração. Em essência, esses indicadores determinam a resposta máxima do sistema na "pior" (mais perigosa) exposição externa e estado inicial, "mencionou o prof. Balandin.
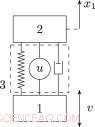
Esquema de proteção contra choque e vibração (sistema de liberdade de grau único). Crédito:Universidade Lobachevsky
Como resultado, São propostos novos métodos e algoritmos para solução numérica de problemas de síntese das leis de controle ótimo de objetos dinâmicos na forma do inverso com os critérios na forma de desvios máximos das saídas do sistema. Como um aplicativo, uma nova classe de problemas de proteção ideal contra choque de vibração de objetos elásticos é considerada, cujos critérios são a deformação máxima do objeto elástico de proteção e a deformação máxima do dispositivo de isolamento de vibração. As tarefas consistem em encontrar feedback caracterizando o absorvedor de vibração e minimizar os critérios acima mencionados em Pareto. Para resolver esta classe de problemas, a abordagem acima mencionada é aplicada a problemas de controle ótimo usando a convolução de Hermeier e a técnica de desigualdades matriciais lineares.
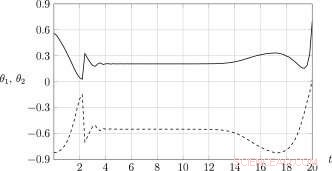
Histórias de tempo dos coeficientes ideais de feedback de estado para sistema de grau único de liberdade. Crédito:Universidade Lobachevsky
A tarefa de dois critérios de proteção ideal contra vibração de um edifício de vários andares contra impactos sísmicos e do vento é considerada em detalhes. Um conjunto de Pareto é construído, bem como uma comparação do Pareto "ideal" do isolador ideal, ou seja, o dispositivo de controle, cujo feedback assume a presença de informações atuais sobre todas as variáveis do estado do sistema mecânico em consideração, com os isoladores ideais de tipos ativos e passivos tendo uma estrutura mais simples do dispositivo de controle.
A aplicação dos métodos desenvolvidos de síntese das leis de controle multicritério ótimo aos problemas de otimização de sistemas de proteção contra choques vibratórios é pioneira e contribui para um avanço significativo na teoria e prática da proteção contra choques vibratórios.