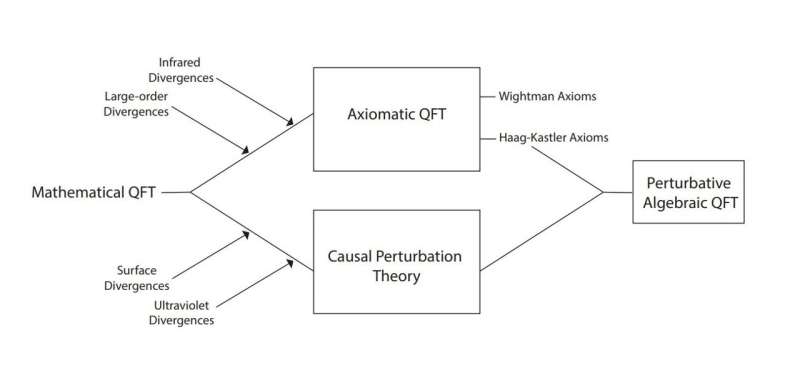
 Representando o QFT algébrico perturbativo (qAQFT) como uma união das vertentes anteriores do QFT axiomático e da teoria da perturbação causal. Crédito:The European Physical Journal H (2024). DOI:10.1140/epjh/s13129-024-00075-6
Representando o QFT algébrico perturbativo (qAQFT) como uma união das vertentes anteriores do QFT axiomático e da teoria da perturbação causal. Crédito:The European Physical Journal H (2024). DOI:10.1140/epjh/s13129-024-00075-6 A expansão perturbativa é uma técnica matemática valiosa amplamente utilizada para quebrar descrições de sistemas quânticos complexos em partes mais simples e gerenciáveis. Talvez o mais importante seja o fato de ter permitido o desenvolvimento da teoria quântica de campos (QFT):uma estrutura teórica que combina princípios da física clássica, quântica e relativística e serve como base do Modelo Padrão da física de partículas.
No entanto, apesar da sua importância na formação da nossa compreensão do universo, o papel da expansão perturbativa tem sido frequentemente subestimado quando se discute os fundamentos matemáticos e filosóficos da QFT. Através de uma nova análise publicada no EPJ H, James Fraser da Universidade de Wuppertal, juntamente com Kasia Rejzner da Universidade de York, trazem o status especial das expansões perturbativas para um foco mais nítido, destacando sua relação profundamente enraizada com os fundamentos do QFT.
As descobertas foram publicadas no The European Physical Journal H .
Na física fundamental, a expansão perturbativa é amplamente usada para extrair previsões experimentais precisas do QFT, que moldaram a teoria à sua forma atual. Mesmo assim, as descrições simplificadas oferecidas pela técnica têm sido amplamente consideradas irrelevantes quando se discute a estrutura matemática e filosófica da teoria.
Em contraste, Fraser e Rejzner argumentam que a matemática da expansão perturbativa desempenhou um papel central no desenvolvimento do QFT:muitas vezes envolvendo-se diretamente com sua estrutura matemática fundamental. Por causa disso, a sua importância não pode ser subestimada quando se discute a natureza fundamental do universo através do QFT.
Por meio do artigo, a dupla traz um foco mais nítido para a história desse relacionamento; traçando a história do uso da expansão perturbativa nos desenvolvimentos fundamentais do QFT. Seu trabalho poderia, em última análise, ajudar os físicos a obter uma compreensão mais profunda das implicações das teorias que desenvolveram usando a expansão perturbativa.
