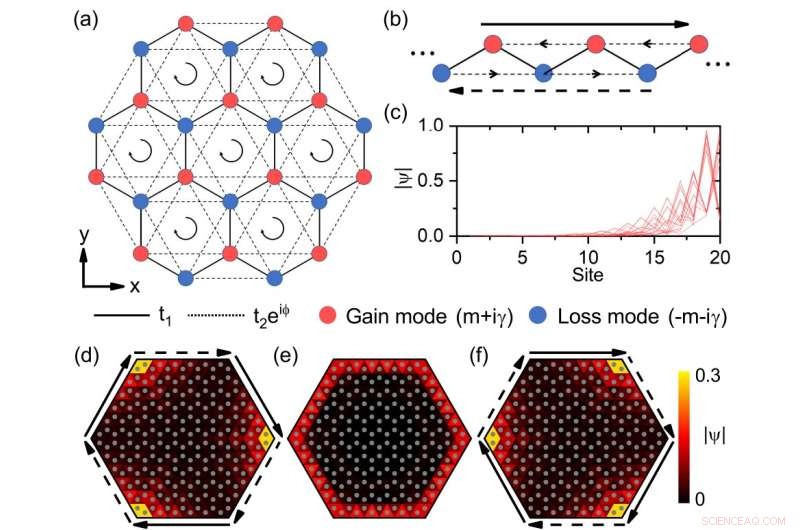
Fig. 1 Modos topológicos de pele híbrida em modelo não-Hermitian Haldane. (a) Esquema da rede não-Hermitiana. Os círculos vermelhos (azuis) denotam locais com termos de massa no local opostos +(m+iγ). (b) Borda em ziguezague da rede em favo de mel como uma cadeia 1D, que tem efeito de pele não-Hermitiano com ganho e perda no local. A longa seta sólida (tracejada) indica a corrente de borda quiral ao longo (oposta) da direção localizada [semelhante em (d) e (f)]. As setas pretas em (a) e as setas de linha média em (b) indicam as direções dos acoplamentos do próximo vizinho mais próximo t2 e
iφ
. (c) Perfil de todos os modos próprios para a cadeia 1D em (b) com 20 sítios. O ganho e a perda no local são γ=3. (d)-(f) O modo de borda quiral para γ=0 (e) torna-se modos topológicos de pele para γ=-0,6 (d) e γ=0,6 (f) com diferentes direções localizadas. Cada triângulo com um círculo cinza denota um site. Aqui o modo de borda quiral se propaga no sentido horário. Crédito:Universidade de Tsinghua
Recentemente, o professor associado Yong-Chun Liu do Departamento de Física e outros descobriram o efeito topológico da pele híbrida induzido por ganho e perda e a transição de fase de paridade-tempo entre os modos topológicos da pele. Os resultados da pesquisa foram publicados em
Cartas de Revisão Física sob o título de "Efeito topológico de pele híbrida induzida por ganho-perda".
Sistemas não Hermitianos são sistemas abertos que podem ser descritos por Hamiltonianos não Hermitianos. Existem muitas novas propriedades em sistemas não-Hermitianos, uma das quais é o efeito da pele não-Hermitiana. Neste efeito, todos os autoestados de um sistema topológico (incluindo estados de massa e estados de borda) são localizados em um dos limites do sistema, e a correspondência convencional de borda de massa é quebrada. Existem basicamente duas maneiras de realizar sistemas não-Hermitianos:uma é usando acoplamentos não recíprocos e a outra é usando ganho e perda.
No caso de acoplamentos não recíprocos, a não-Hermiticidade vem da natureza não-Hermitiana da interação entre os diferentes sítios da rede. A troca de energia entre os sítios da rede é assimétrica, então há um fluxo de energia líquida em uma direção e toda a energia é finalmente reunida na fronteira. Assim, os sistemas não recíprocos exibem o efeito pelicular. No caso de ganho-perda, a não-Hermiticidade se origina do ganho e da perda em cada sítio da rede, o que equivale a adicionar energia imaginária no sítio a cada sítio da rede. Este tipo de sistema não-hermitiano nem sempre leva ao efeito da pele. Em sistemas realistas, os acoplamentos não recíprocos são geralmente difíceis de alcançar, mas a dissipação é generalizada e a distribuição escalonada da dissipação é equivalente a ganho e perda. Portanto, é de grande importância estudar o efeito da pele em sistemas não-Hermitianos de ganho-perda.
Eles encontraram o efeito topológico da pele híbrida induzido por ganho e perda em sistemas bidimensionais. Esse tipo de efeito pelicular é seletivo, ou seja, os estados bulk e os estados de borda têm comportamento diferente. Os estados de volume não são afetados pelo efeito de pele e permanecem estendidos, enquanto os estados de borda exibem efeito de pele e são localizados nos cantos. Este fenômeno híbrido de efeito pelicular e efeito topológico mostra as propriedades únicas de sistemas topológicos não-Hermitianos, que não possuem análogos Hermitianos ou não-topológicos.
Como exemplo específico, eles consideraram o modelo Haldane não-Hermitiano com ganho e perda [Fig. 1(a)]. No modelo Haldane, os estados topológicos de borda são obtidos pela introdução de energia no local e fluxo magnético local. É um dos dois modelos importantes para realizar o efeito Hall anômalo quântico na física da matéria condensada. Eles descobriram que se ganho e perda escalonados são introduzidos nos locais vizinhos mais próximos no modelo Haldane, os modos de borda topológica do sistema exibirão o efeito de pele e serão localizados nos cantos, enquanto os modos de massa não serão afetados. Assim, revela um efeito híbrido da topologia da pele.
Ao analisar os sítios da rede apenas nas bordas, esse efeito topológico de pele de segunda ordem pode ser simplificado para o efeito de pele de primeira ordem nas bordas. No modelo unidimensional simplificado, existem correntes de borda quirais devido ao fluxo magnético não local introduzido pelos acoplamentos complexos do próximo vizinho mais próximo. Eles são equivalentes a acoplamentos não recíprocos, de modo que o sistema exibe o efeito pelicular de primeira ordem [Fig. 1 (b)—(c)]. Ao contrário, há apenas fluxo local, e a não reciprocidade se anula no grosso do sistema. Portanto, os modos em massa não são afetados pelo efeito de pele. Ao ajustar o ganho e a perda do sistema, a direção das correntes de borda pode ser alterada, para controlar a direção do efeito topológico da pele [Fig. 1 (d)—(f)].
Eles obtiveram ainda a relação entre as simetrias de paridade-tempo (PT) do sistema e o efeito topológico da pele híbrida. Ao escolher a condição de contorno aberta e a condição de contorno periódica em diferentes direções, o sistema exibe diferentes tipos de simetrias PT para diferentes tipos de arestas. A simetria PT global que mapeia qualquer modo localizado em uma fronteira na outra fronteira impede a emergência do efeito topológico pele híbrido, enquanto a simetria PT local com mapeamento dentro de cada sub-célula permite a existência do efeito topológico pele híbrido.
Portanto, a análise das simetrias de PT do sistema fornece um meio simples e eficaz para julgar se existe o efeito híbrido pele-topológico. Em particular, eles descobriram que quando o ganho e a perda no sistema aumentam, a transição de fase PT ocorrerá entre os modos topológicos da pele, acompanhada pelo surgimento de pontos excepcionais (EPs). Quando a simetria do PT é quebrada, as energias próprias dos modos topológicos da pele não são mais reais e as distribuições dos modos próprios correspondentes tornam-se assimétricas do PT.
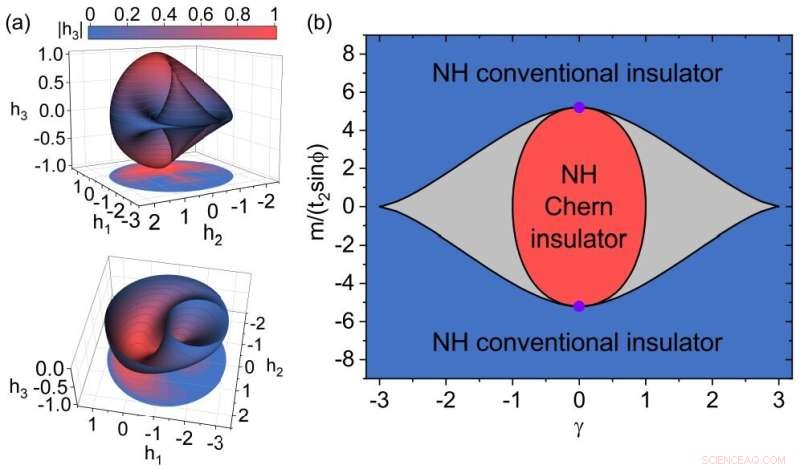
Fig. 2 A topologia e diagrama de fases do modelo Haldane não-Hermitiano. (a) A superfície S mapeada da primeira zona de Brillouin, ou seja, mapeando de (kx , ks ) a (h1 , h2 , h3 ). The color map represents the magnitude of h3 . The density map below is the projection of the surface. The bottom figure is half of the top figure for h3 <0. (b) The phase diagram. The red area is the non-Hermitian Chern insulator phase where C=1. The blue area is the non-Hermitian conventional insulator phase where C=0. The gray area is a gapless phase with EPs between two bulk bands. The black curves are phase boundaries. The purple points indicate the Hermitian phase boundary with the emergence of Dirac points. Credit:Tsinghua University
In addition, they studied the Chern numbers in the non-Hermitian system and obtained the phase diagram. They provided intuitionistic geometric meanings of the Chern numbers as topological invariants. As shown in Fig. 2(a), the two-dimensional Brillouin zone of the system can be mapped to a closed spherical surface S in the three-dimensional space, and the gap-closing points of the system form a circle L in the three-dimensional space. When the surface S encloses the circle L, the system is at the non-Hermitian Chern insulator phase, and the Chern number is 1, corresponding to the red region in Fig. 2(b). When the circle L is outside the surface S, the system is at the non-Hermitian conventional insulator phase, and the Chen number is 0, corresponding to the blue area in Fig. 2 (b). In the gray area in Fig. 2 (b), the system band gap is closed at six EPs.
The conclusion of this work is also applicable to the system with no gain and only pure dissipation. Dissipation is common in many physical systems, such as optical systems, atomic systems, and optomechanical systems. This work paves the way to realize non-Hermitian topological effect by gain and loss and study PT phase transition in higher-dimensional systems. It also provides attractive insights for potential applications in topological optics.
+ Explorar mais An approach for constructing non-Hermitian topological invariants in real space

