Modelo teórico que descreve o movimento das ondas de ultrassom na presença de várias bolhas
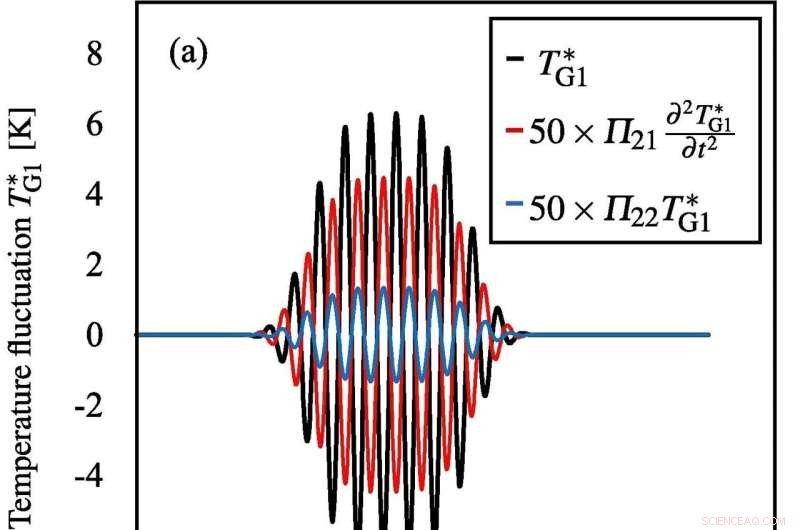
Desenvolvimento temporal da flutuação de temperatura TG1
∗
(a) na fonte sonora (condição de contorno) e (b) no foco da Fig. 3 (a), onde o gás dentro da bolha é Argônio. As curvas preta, vermelha e azul representam as formas de onda da flutuação de temperatura, o termo de dissipação devido à viscosidade interfacial e compressibilidade do líquido, e o termo de dissipação devido à condutividade térmica do gás. Crédito:Sonoquímica Ultrassônica (2022). DOI:10.1016/j.ultsonch.2022.105911
Cientistas da Escola de Pós-Graduação de Sistemas e Engenharia da Informação da Universidade de Tsukuba criaram um modelo teórico para descrever o movimento das ondas de ultrassom na presença de várias bolhas. Este trabalho pode ajudar os médicos a projetar novas aplicações diagnósticas e terapêuticas da tecnologia de ultrassom.
Tratamentos médicos de ultra-som focalizado para ablação de tumores ou quebra de cálculos renais com litotripsia por ondas de choque podem oferecer a chance de melhores resultados do paciente sem exposição à radiação eletromagnética ou de partículas. No entanto, esses métodos dependem de uma compreensão da maneira como as ondas de ultrassom se movem em ambientes complexos, como tecidos vivos. Isso é especialmente verdadeiro para a terapia de ablação tumoral, que funciona direcionando o calor criado pelo ultrassom para destruir as células doentes. Equações de propagação de ondas mais completas são necessárias para garantir que essas modalidades estejam sendo implementadas corretamente.
Agora, cientistas da Universidade de Tsukuba estenderam o modelo convencional de propagação de ondas sonoras para incluir várias bolhas. A equação de Khokhlov-Zabolotskaya-Kuznetsov (KZK) foi usada anteriormente como um modelo simplificado para a propagação não linear de ultra-som focalizado em um líquido puro. Ser capaz de escrever uma única equação para modelar ultra-som não linear, oscilações de bolhas e flutuação de temperatura de maneira consistente abre o caminho para aplicações médicas aprimoradas por microbolhas.
"Um modelo matemático para aplicações médicas utilizando bolhas deve descrever a não linearidade da propagação do ultrassom e da oscilação das bolhas", diz o autor Professor Tetsuya Kanagawa. Os cientistas usaram um método de combinar escalas de vários tamanhos calculando as equações básicas médias volumétricas para líquidos borbulhantes. As equações resultantes tinham termos para efeitos não lineares, dissipação de som, dispersão e foco. Em particular, o próprio termo de dissipação dependeu de três fatores:viscosidade interfacial do líquido, compressibilidade do líquido e a condutividade térmica do gás dentro das bolhas.
"Em refinamentos futuros, podemos adicionar extensões teóricas da equação KZK que incorporam os efeitos viscosos do líquido a granel, a elasticidade dos tecidos do corpo e a transferência de calor", diz o professor Kanagawa. Uma aplicação inicial é o uso de microbolhas como agentes de contraste para melhorar a resolução das imagens de ultrassom. No entanto, eles também podem ser estendidos a intervenções que realizam a ablação direcionada de tecidos.
+ Explorar mais A impressão direta de som é um potencial divisor de águas na impressão 3D, de acordo com pesquisadores
