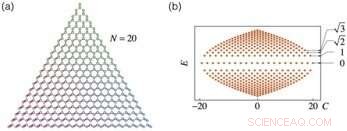
uma. SL com forças de acoplamento variáveis no local. b. Espectro de energia do FSL. Crédito:Science China Press
Desde a descoberta do efeito Hall quântico, As fases topológicas dos elétrons se tornaram uma importante área de pesquisa na física da matéria condensada. Muitas fases topológicas são previstas em redes com engenharia específica de salto eletrônico entre locais de rede. Infelizmente, a distância entre locais vizinhos em redes naturais (cristais) é da ordem de um bilionésimo de metro, o que torna essa engenharia extremamente difícil. Por outro lado, os cristais fotônicos têm uma escala muito maior. As células unitárias dos cristais fotônicos para a luz visível são milhares de vezes maiores do que as dos elétrons. Portanto, não é surpreendente que as pessoas recorram ao analógico fotônico de fases topológicas, descobrindo a semelhança entre as equações de Maxwell e Schrodinger, e uma área de pesquisa chamada fotônica topológica floresceu.
Contudo, fótons e elétrons são tão diferentes quanto cães e gatos. Os fótons são sociais por natureza. Eles adoram ficar juntos (é por isso que temos lasers). Os elétrons se odeiam. Eles têm seus próprios territórios de acordo com o princípio de exclusão de Fermi. A fotônica topológica baseada no análogo entre as equações de Maxwell e Schrodinger pertence à óptica clássica, ou seja, uma simulação de onda clássica da topologia de banda eletrônica. É natural perguntar se a luz quantizada incorpora novas fases topológicas além da interpretação da óptica clássica. Recentemente, Han Cai e Da-Wei Wang da Universidade de Zhejiang revelaram as fases topológicas em redes de estados quantizados de luz.
A energia da luz só pode existir em pacotes discretos, um número inteiro não negativo mais a metade de hν, onde h é a constante de Planck e ν é a frequência da luz. O inteiro é o número de fótons nesse estado, que é chamado de estado Fock, e a outra metade é contribuída pelas flutuações do vácuo. Esta discrição da energia da luz é a chave para explicar os espectros da radiação do corpo negro (por exemplo, em uma fornalha, temperatura mais alta muda o espectro para o lado azul de uma faixa de arco-íris). A quantização da luz também tem consequências profundas nas interações átomo-fóton. Quando há n fótons no campo de luz, a probabilidade de um átomo excitado emitir outro fóton é proporcional a n + 1 (lembre-se de que os fótons são sociais e eles adoram que novos membros participem). Quando a luz está confinada em uma cavidade, a energia emitida pelo átomo pode ser reabsorvida, que resulta em uma oscilação do átomo entre os estados excitado e fundamental, e a frequência de oscilação é proporcional à raiz quadrada de n + 1. Um espectro desses valores discretos das frequências de oscilação pode ser observado quando o átomo é acoplado à luz em uma superposição de estados de Fock, ou seja, no modelo Jaynes-Cummings (JC), que se tornou um método padrão na obtenção dos estados quânticos da luz.
Não é óbvio que o modelo JC está relacionado a fases topológicas, mas esta escala de raiz quadrada de inteiro do espectro de energia é uma reminiscência dos níveis de Landau de elétrons em um grafeno, que é o berço das fases topológicas. As bandas de energia dos elétrons em um grafeno tocam em dois pontos na borda da zona de Brillouin, chamados de pontos Dirac, onde os elétrons obedecendo à equação bidimensional de Dirac têm uma relação linear entre sua energia e momento. Quando um campo magnético é aplicado, os elétrons fazem movimentos de cíclotron com frequências discretas escalonadas com a raiz quadrada de inteiros, que correspondem a níveis discretos de Landau. Cai e Wang estabeleceram a conexão entre o modelo JC de três modos e os elétrons de Dirac em um campo magnético.
Em um modelo JC de três modos, onde um átomo é acoplado a três modos de cavidade, os estados quânticos podem ser totalmente descritos por quatro inteiros (x, y, z, q), onde x, y e z são os números dos fótons nos três modos de cavidade, e q =0 e 1 para os estados fundamental e excitado do átomo. No modelo JC, todos os (N + 1) ^ 2 estados que satisfazem x + y + z + q =N formam uma rede de favo de mel, semelhante a um grafeno e nós o chamamos de rede do estado de Fock. Uma vez que o átomo excitado pode emitir um fóton para um dos modos de cavidade, o estado (x, y, z, 1) é acoplado a três estados vizinhos, (x + 1, y, z, 0), (x, y + 1, z, 0) e (x, y, z + 1, 0). Contudo, as intensidades de acoplamento aos três modos de cavidade são proporcionais à raiz quadrada de seus números de fótons. Para cada estado (x, y, z, 1) há competição entre as três cavidades para a obtenção do fóton emitido pelo átomo, e as cavidades que contêm mais fótons têm uma vantagem, que pode ser entendido como o princípio da maioria dos fótons. Isso é equivalente a um grafeno submetido a uma deformação que modifica os coeficientes de salto dos elétrons de um local para seus três vizinhos.
Acontece que quando a força de acoplamento entre o modo de cavidade mais populosa e o átomo é maior do que a soma dos outros dois modos, os dois pontos de Dirac se fundem e uma lacuna de banda se abre, que é uma transição topológica de Lifshitz entre um semimetal e um isolador de banda. Na fase semimetálica, a variação da força de acoplamento é equivalente a um campo de deformação que induz um campo magnético efetivo e leva a níveis de Landau quantizados, com base no qual os autores investigaram o efeito Hall do vale e construíram um modelo Haldane no modelo JC de três modos.
Os autores também investigaram as redes de estado de Fock unidimensionais com apenas dois modos de cavidade. Eles são modelos Su-Schriefer-Heeger intrínsecos e hospedam estados de borda topológicos. O modelo pode ser estendido para mais de três dimensões para fases topológicas indisponíveis em redes reais. As fases topológicas propostas estão prontas para serem realizadas em circuitos supercondutores e são promissoras para aplicações em processamento de informação quântica.