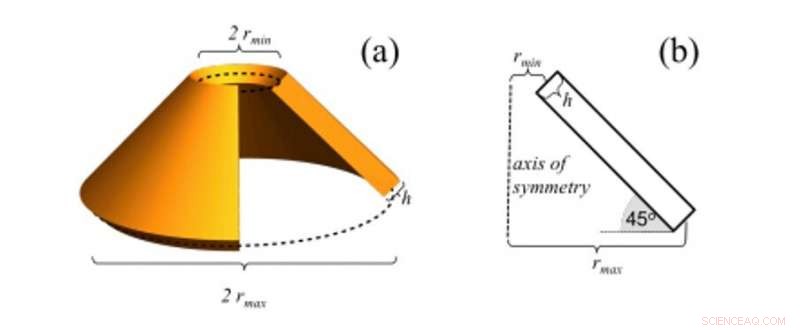
Um esboço do cone viscoelástico, e suas dimensões. (a) Uma vista em ângulo com uma seção da casca cônica recortada. (b) Um diagrama em seção transversal incluindo o eixo de simetria e uma seção única da casca cônica. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Atualmente é desafiador determinar a estabilidade de estruturas viscoelásticas, uma vez que conformações aparentemente estáveis podem se arrastar gradualmente (deformação plástica de um material sob tensão em função do tempo) até que sua estabilidade seja perdida. Embora um efeito de deslizamento perceptível não leve necessariamente à instabilidade de sólidos viscoelásticos, os pesquisadores estão atualmente limitados com simulações numéricas para prever a estabilidade futura em relação às ferramentas preditivas teóricas. Em um novo relatório sobre Avanços da Ciência , Erez Y. Urbach e Efi Efrati em física e sistemas complexos no Weizmann Institute of Science, Israel, descreveu sólidos viscoelásticos por meio de uma métrica de referência instantânea em evolução para medir deformações elásticas. Os métodos transparentes e intuitivos derivados neste trabalho para sólidos viscoelásticos incompressíveis reduziram a questão da estabilidade futura apenas a cálculos estáticos. A equipe mostrou o poder preditivo da abordagem ao compreender os mecanismos sutis de instabilidade retardada em cascas elastoméricas finas, a fim de demonstrar concordância quantitativa com os experimentos.
Movimento rastejante na natureza
Um movimento rasteiro relativamente lento está por trás da armadilha da mosca de Vênus - um dos movimentos mais rápidos no reino vegetal. Deformação semelhante é observada antes do rompimento de cascas elastoméricas finas, conhecidos como saltadores que duram uma fração de segundo. Embora o movimento lento de arrastamento das conchas pareça ser elasticamente estável, durando ordens de magnitude mais, aqueles em uma escala muito maior podem ser observados na crosta terrestre antes de um terremoto posterior. Os pesquisadores ainda estão aprendendo o papel exato da viscoelasticidade em tremores secundários devido à ausência de uma estrutura teórica preditiva para detectar a estabilidade futura de tais sistemas. Em cada um dos exemplos descritos, o fluxo viscoelástico lento no material pode levar o sistema a instabilidades, causando uma liberação abrupta de energia elástica armazenada internamente. Embora os cientistas possam determinar as variáveis que governam o comportamento viscoelástico, os mecanismos de instabilidades retardadas em fluidos viscoelásticos permanecem pouco compreendidos. Nesse trabalho, Urbach e Efrati abordaram quantitativamente a característica de instabilidade viscoelástica usando uma descrição métrica.
Representação esquemática da colinearidade das métricas. A minimização da métrica g (marcada por um círculo preto completo) é restrita e executada em relação ao subconjunto de métricas que correspondem às configurações realizáveis (linha preta grossa). Essas métricas estão em, especial, preservação da orientação e euclidiana. Dada uma métrica de referência instantânea, g¯ (marcado por um círculo cinza completo), a métrica realizada corresponderá ao ponto mais próximo do conjunto de métricas admissíveis a g¯ de acordo com a função de distância dada pela energia elástica instantânea. Começando do descanso, g¯ evolui de g¯0 (marcado por um círculo vermelho completo) em direção a g, que permanece a métrica admissível mais próxima de g¯ devido à colinearidade das três métricas. Como g permanece estacionário, a evolução de g irá preservar a colinearidade, aproximando-se assintoticamente de g¯stat (marcado por um círculo aberto), que também é colinear. Ressaltamos que ao longo dessa evolução, g permanece inalterado; portanto, nenhuma variação da configuração será observada, apesar do relaxamento de tensão. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948 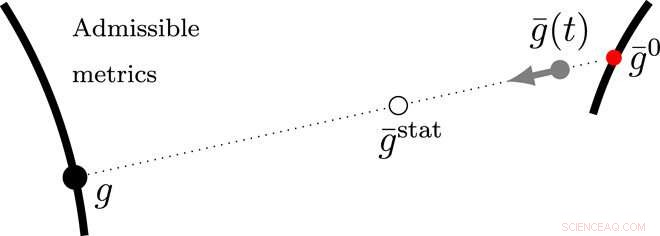
A equipe descreveu o comportamento dos materiais como uma resposta elástica rápida em relação aos comprimentos de teste em evolução temporal que podem mudar devido ao fluxo viscoelástico lento. Eles interpretaram a resposta microscópica no material e previram a estabilidade futura de estruturas viscoelásticas irrestritas. Urbach et al. explicou todas as relações de materiais viscoelásticos lineares por meio de cálculos intrincados de taxa de deformação com uma função de relaxamento de tensão, em seguida, derivou relações matemáticas para sistemas unidimensionais neste trabalho; alguns dos quais dependiam de propriedades materiais, como o módulo de Young e o coeficiente de Poisson. Deformações incrementais instantâneas causaram aumento da tensão linear para uma resposta puramente elástica no material. Uma vez que os materiais viscoelásticos tendem a ser dissipativos (termodinamicamente abertos), a definição de uma energia livre elástica pode ser incompleta. Os cientistas, portanto, eliminaram a inércia do sistema e aproximaram o movimento do material a um quase-estado que evolui entre estados de equilíbrio elástico. Como resultado, uma dada métrica de referência instantânea pode render múltiplas configurações elasticamente estáveis.
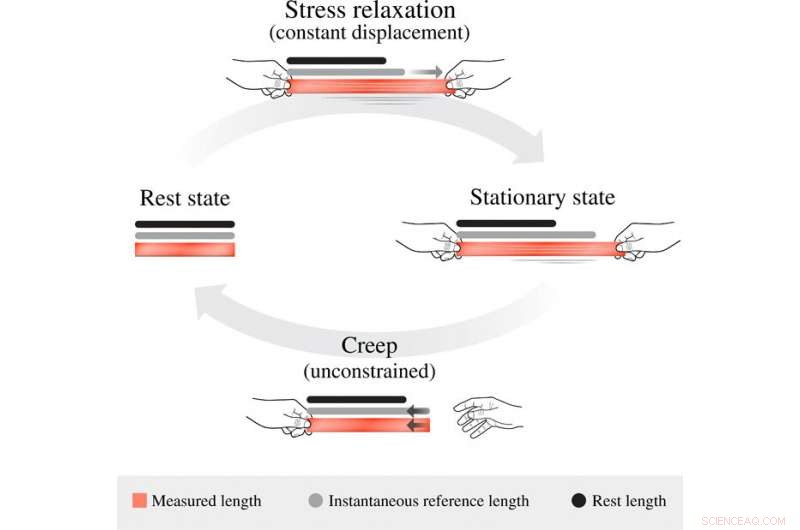
A evolução do comprimento de referência viscoelástica. No estado de repouso, todas as três medidas de comprimento no corpo, seu comprimento medido g (marcado em vermelho), seu comprimento de referência instantâneo g¯ (marcado em cinza), e seu comprimento de referência de repouso g¯0 (marcado em preto) são todos iguais. Quando sujeito a uma extensão de deslocamento constante, o comprimento de referência instantâneo evolui para longe do comprimento de descanso e em direção ao comprimento atualmente assumido, resultando assim em relaxamento de estresse. Ele se aproxima assintoticamente do estado estacionário g¯stat =βg + (1 − β) g¯0, em que a tensão inicial é reduzida por um fator de 1 - β. Quando lançado, o sistema irrestrito adota imediatamente seu comprimento de referência instantâneo preferido, que, por sua vez, gradualmente se arrasta em direção aos comprimentos de descanso. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Instabilidades viscoelásticas por meio da descrição da métrica
A métrica de referência instantânea dependente do tempo do material poderia, desta forma, evoluir para adquirir novas configurações estáveis, mesclar os pontos estáveis existentes, ou fazer com que as configurações elásticas estáveis percam a estabilidade. No último cenário, a lenta evolução viscoelástica será seguida por um rápido snap - destacando a principal dificuldade de prever a estabilidade das estruturas viscoelásticas. Este recurso é conhecido como biestabilidade temporária, pseudo-biestabilidade ou flambagem por fluência. Dois processos distintos devem ocorrer para que sólidos viscoelásticos lineares incompressíveis se tornem instáveis. Primeiro, um estado elasticamente estável adquirirá estabilidade por meio do relaxamento viscoelástico sob alguma carga externa por um período de tempo. Então, quando a carga externa é removida, o corpo assumirá o estado estável recém-adquirido, ao lado de fluência viscoelástica para a instabilidade resultante. Contudo, um estado estável adquirido é transitório (temporário). Desta maneira, Urbach et al. usou a descrição métrica de viscoelasticidade para fornecer uma imagem do mecanismo que governa a estabilidade de estruturas viscoelásticas.
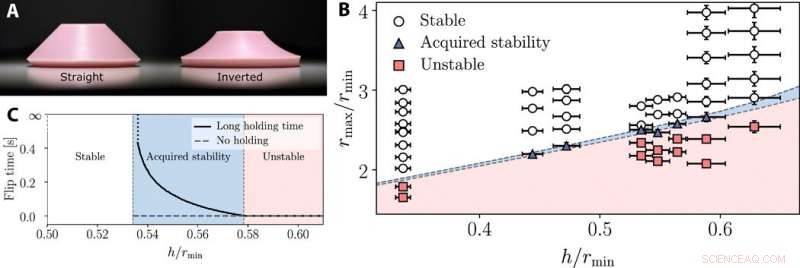
Verificação experimental do diagrama de estabilidade viscoelástica. (A) Poppers cônicos retos e invertidos. Crédito da foto:Erez Y. Urbach, Instituto Weizmann. (B) Os dois eixos abrangem as propriedades geométricas adimensionais dos poppers cônicos truncados. As cores de fundo representam as regiões teoricamente previstas de cada uma das fases. Cada marcador corresponde a um popper diferente; marcadores de diferentes formatos (e coloridos) indicam as diferentes fases observadas no experimento. (C) Tempo de rotação calculado numericamente como uma função da espessura normalizada do popper cônico para liberação imediata e longo tempo de espera. Os diferentes poppers foram simulados variando suas espessuras e raios constantes rmin =10 mm, rmax =25 mm. As propriedades do material tomadas foram β =0,1, e o kernel da memória foi assumido como exponencial com τ =0,1 s, Módulo de Young E =2,5 MPa, e coeficiente de Poisson v =0,47. A variação do kernel pode levar a uma taxa variável de divergência do tempo de inversão entre a região de estabilidade estável e adquirida, no entanto, a localização dessa divergência permanecerá inalterada. A divergência dos tempos de inversão foi abordada em um estudo anterior, e mais recentemente, a taxa de divergência também foi estudada anteriormente. Crédito:Science Advances, doi:10.1126 / sciadv.abb2948
Resultados experimentais
Os cálculos realizados neste trabalho revelaram muitas características qualitativas das instabilidades viscoelásticas. Os cientistas então testaram as previsões quantitativas da teoria examinando experimentalmente a resposta dos poppers cônicos de borracha de silicone. Por esta, eles moldam poppers de borracha de silicone como conchas cônicas truncadas para obter um controle mais simples sobre a espessura do material. Conforme a espessura aumentou, a biestabilidade diminuiu, então, em um ponto no tempo, o popper imediatamente voltou. Os cientistas produziram 50 poppers cônicos diferentes de geometrias diferentes e testaram suas fases para determinar experimentalmente os limites de fase das propriedades viscoelásticas.
O trabalho aqui apresentado foi semelhante a estudos anteriores sobre elastoplasticidade. A teoria métrica pode ser implementada para sólidos viscoelásticos incompressíveis isotrópicos para fornecer regras básicas para instabilidades viscoelásticas. Para que uma determinada estrutura entre em instabilidade, o deslizamento deve ter precedido dentro de um período de tempo em que as estruturas foram mantidas sob uma carga externa. A teoria foi especificamente poderosa na aplicação para descrever a instabilidade experimentalmente retardada em cascas elastoméricas finas. Esses resultados serão capazes de lançar luz sobre o papel da viscoelasticidade no desencadeamento de terremotos posteriores. Desta maneira, a descrição da métrica aqui proposta fornecerá um arcabouço teórico para entender as instabilidades viscoelásticas retardadas.
© 2020 Science X Network