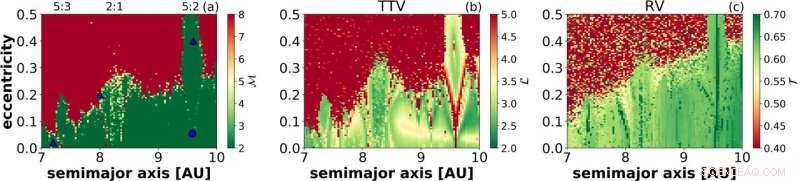
Um mapa de estabilidade de Saturno obtido pelo indicador de caos MEGNO (a) e rede de recorrência mede o comprimento médio do caminho (b) e a transitividade (c). Os dois últimos painéis são baseados na variação do tempo de trânsito de Júpiter e na velocidade radial do sol, respectivamente. Crédito:Tamás Kovács
Exoplanetas girando em torno de estrelas distantes estão entrando rapidamente em foco com tecnologia avançada como o telescópio espacial Kepler. É difícil obter um entendimento completo desses sistemas, porque as posições e velocidades iniciais dos exoplanetas são desconhecidas. Determinar se a dinâmica do sistema é quase periódica ou caótica é complicado, caro e exigente do ponto de vista computacional.
Nesta semana Caos , Tamás Kovács oferece um método alternativo para análise de estabilidade de corpos exoplanetários usando apenas os dados de série de tempo observados para deduzir medições dinâmicas e quantificar a imprevisibilidade de sistemas exoplanetários.
"Se não conhecermos as equações que regem o movimento de um sistema, e temos apenas a série temporal - o que medimos com o telescópio - então queremos transformar essa série temporal em uma rede complexa. Nesse caso, é chamada de rede de recorrência, "Kovács disse." Esta rede contém todas as características dinâmicas do sistema subjacente que queremos analisar. "
O artigo baseia-se no trabalho do físico Floris Takens, que propôs em 1981 que a dinâmica de um sistema poderia ser reconstruída usando uma série de observações sobre o estado do sistema. Com o teorema de incorporação de Takens como ponto de partida, Kovács usa a incorporação de atraso de tempo para reconstruir uma trajetória de alta dimensão e, em seguida, identificar pontos de recorrência, onde os corpos no espaço de fase estão próximos uns dos outros.
“Esses pontos especiais serão os vértices e as bordas da complexa rede, "Kovács disse." Assim que você tiver a rede, você pode reprogramar esta rede para poder aplicar medidas como transitividade, comprimento médio do caminho ou outros exclusivos dessa rede. "
Kovács testa a confiabilidade do método usando um sistema conhecido como modelo, o sistema de três corpos de Saturno, Júpiter e o sol, e, em seguida, aplica-o ao sistema Kepler 36b e 36c. Os resultados do sistema Kepler estão de acordo com o que se sabe.
"Estudos anteriores apontaram que Kepler 36b e 36c é um sistema muito especial, porque a partir da simulação direta e das integrações numéricas, vemos que o sistema está à beira do caos, "Kovács disse." Às vezes, mostra uma dinâmica regular, e em outras ocasiões, parece ser caótico. "
O autor planeja em seguida aplicar seus métodos a sistemas com mais de três corpos, testar sua escalabilidade e explorar sua capacidade de lidar com séries temporais mais longas e conjuntos de dados mais nítidos.