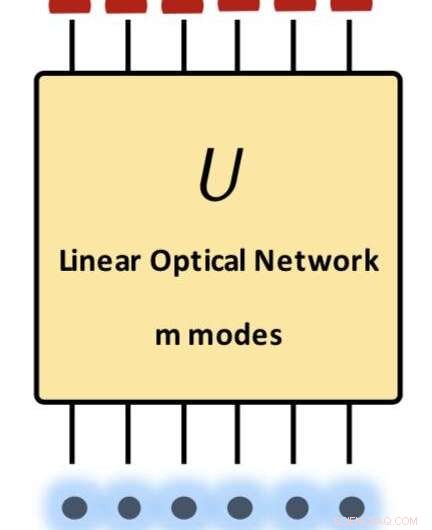
Resumo do nosso resultado principal:um limite superior das amplitudes de transição para óptica linear. Os estados inicial e final são produtos dos estados Fock. A matriz U apresenta qualquer transformação unitária realizável em óptica linear. Crédito:Science China Press
A ótica linear é um dos melhores exemplos para demonstrar a física quântica. Funciona à temperatura ambiente, e pode ser observado com dispositivos relativamente simples. A óptica linear envolve processos físicos que conservam o número total de fótons. No caso ideal, se houver 100 fótons no início, não importa o quão complicado seja o processo físico, sobrarão exatamente 100 fótons no final.
Os fótons são partículas bosônicas não interagentes. Contudo, eles ainda podem interferir uns com os outros, exibindo efeitos quânticos não triviais. Um exemplo típico é o experimento de Hong-Ou-Mandel, onde dois fótons idênticos são enviados para um dispositivo experimental. Depois de uma transformação linear simples, os dois fótons aparecem como se estivessem grudados e sem vontade de se separar. Além de fornecer uma compreensão básica da mecânica quântica, o estudo da óptica linear também levou a muitas aplicações científicas.
Nos últimos anos, as propriedades únicas dos sistemas ópticos lineares também inspiraram o desenvolvimento da teoria da complexidade computacional. Em 2012, O professor Scott Aaronson do MIT (atualmente na Universidade do Texas em Austin) propôs um método ótico linear para demonstrar a supremacia quântica (computacional), que é baseado no conceito de amostragem de bóson. Mais especificamente, Aaronson sugeriu que, para uma classe de problemas de amostragem com base em sistemas ópticos lineares, seria impossível, na prática, aplicar qualquer computador clássico para simular. Essa ideia imediatamente dá início a uma corrida para alcançar o status de "supremacia quântica". Muitos laboratórios de óptica quântica em todo o mundo se interessaram em desenvolver sistemas de amostragem de bósons para quebrar recordes em termos de números de fótons. Por outro lado, os cientistas da computação estão ocupados aplicando supercomputadores para elevar o nível de conquista da supremacia quântica.
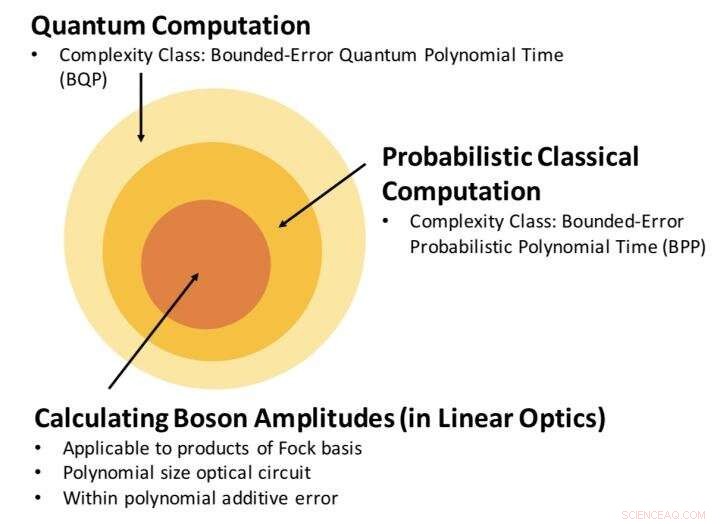
Relação entre a classe de complexidade de estimativa da amplitude do bóson, e computação clássica e quântica. Nosso resultado estabelece que calcular a amplitude do bóson, com um erro aditivo polinomial, é um problema dentro do BPP. Crédito:Science China Press
Contudo, em termos de problemas práticos, aplicar o modelo de amostragem de bóson não é uma boa abordagem. Portanto, Aaronson levantou uma questão em 2012:além dos problemas de amostragem, os pesquisadores podem explorar a óptica linear para alcançar a supremacia quântica em termos de problemas de decisão com uma resposta SIM / NÃO? Recentemente, Prof. Man-Hong Yung, professor associado da SUSTech e seus colegas publicaram um artigo intitulado "Limite universal na amostragem de bósons em óptica linear e suas implicações computacionais" em National Science Review ( NSR ), oferecendo uma solução completa para o problema aberto colocado por Aaronson.
Especificamente, A equipe de Yung descobriu um limite fundamental nas probabilidades de transição de sistemas ópticos lineares, restringindo a capacidade de transferir bósons usando dispositivos ópticos lineares. Junto com as ferramentas da óptica quântica, eles desenvolveram um algoritmo clássico que pode estimar com eficiência a amplitude de transição com um erro limitado. Consequentemente, esses resultados levam a uma resposta negativa ao problema aberto de Aaronson. Em outras palavras, para codificar problemas de decisão difícil, é necessário fazer uso de sistemas de óptica quântica mais complicados em vez de apenas óptica linear.
Como um domínio interdisciplinar entre a física quântica e a ciência da computação, a ciência da informação quântica continua a ser uma área de pesquisa altamente ativa. Por um lado, os resultados da equipe de Yung contribuem para a fundamentação teórica da óptica quântica; por outro lado, além da amostragem de bóson, esses resultados apontam para uma nova perspectiva sobre problemas de complexidade computacional em termos de óptica quântica. Sem dúvida, no futuro, devemos esperar ver muitos resultados mais empolgantes como esses nesta área.