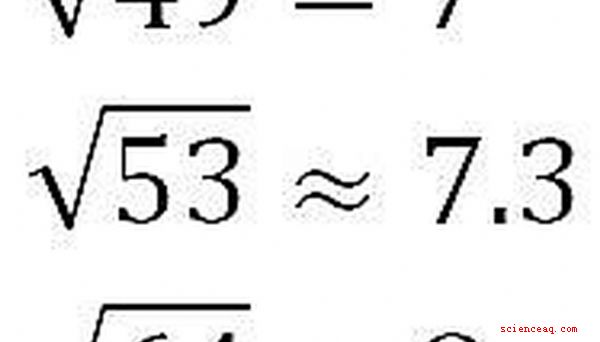
Em matemática, às vezes é importante estimar os valores de raízes quadradas (radicais). Este é especialmente o caso em exames que não permitem o uso de uma calculadora, e você está tentando eliminar respostas erradas, ou verificar a razoabilidade de sua resposta. Além disso, na geometria, os valores sqrt (2) e sqrt (3) surgem com tanta freqüência que é essencial conhecer seus valores aproximados.

Este artigo mostra as etapas para estimar uma raiz quadrada. O artigo pressupõe que você tenha uma compreensão básica de raízes quadradas e quadrados perfeitos. Consulte a seção Referência para obter mais informações.

Para estimar o valor da raiz quadrada de um número, encontre os quadrados perfeitos acima e abaixo do número. Por exemplo, para estimar o sqrt (6), note que 6 é entre os quadrados perfeitos 4 e 9. Sqrt (4) = 2 e sqrt (9) = 3. Como 6 é mais próximo de 4 do que 9, Eu esperaria que sua raiz quadrada estivesse mais próxima de 2 do que de 3. Na verdade, é cerca de 2.4, mas contanto que você soubesse que era nesse estádio, você ficaria bem. Mesmo sabendo que era algo entre 2 e 3 seria a sua vantagem.

Vamos tentar outro exemplo. Estimar o sqrt (53). 53 está entre os quadrados perfeitos 49 e 64, cujas raízes quadradas são 7 e 8, respectivamente. 53 está mais perto de 49 do que para 64, então seria razoável estimar o sqrt (53) entre 7 e 7.5. Acontece que é cerca de 7,3.

Existem duas raízes quadradas que surgem com muita frequência na geometria. Eles são sqrt (2) e sqrt (3). É muito importante que você memorize seus valores aproximados. Note que sqrt (1) é 1, e sqrt (4) é 2. Com base nisso, não é surpresa que sqrt (2) seja aproximadamente 1.4 e sqrt (3) seja aproximadamente 1.7.

O mais importante é lembrar que sqrt (2) é maior que 1, e sqrt (3) é menor que 2. Outro artigo discute a aplicação dessas raízes quadradas no trabalho com triângulos retângulos e o Teorema de Pitágoras.

Os alunos devem se certificar de que estão confortáveis ​​em estimar as raízes quadradas e, por esse motivo, estimar todas as suas respostas para ver se são razoáveis. Isso geralmente permite que você pegue seus erros antes de entregar seus exames.